The Fabric of Reality Handbook
Basically a whole another book clearly and comprehensively explaining and summarizing The Fabric of Reality and its main ideas chapter by chapter.
🐣 0 — Introduction
A Word for Your Journey
I aim to concisely explain key points of the book, each chapter should take you around 30 minutes.
The best way to retain and incorporate ideas is to constantly challenge your understanding. Hence, chapters are structured by their main questions, after reading, you can practice them all as flashcards here.
I recorded summaries of all chapters as one podcast, you can listen to it above. You also can listen to my interview with Elias Schlie where we explore the main ideas of both The Beginning of Infinity, and The Fabric of Reality in 3 hours. Lastly, I made a public playlist with Brett Hall’s lectures in book’s order: you can listen to it here.
As a different medium you can read this handbook in Notion with toggled questions and chapters. (I’m working on a pdf version.)
The Fabric of Reality was a very rewarding and challenging read for me. I hope my work makes it easier to understand David’s ideas without diminishing their value. When in hardship — persevere, the fruits of understanding taste sweet.
My handbook is no substitute for reading the book, nothing is. It is a companion along your journey.
By endurance we conquer, Mark
🎯 5-Minute Summary
To change the world we first must understand it. To understand it we must take our best scientific theories seriously and jointly. These are: epistemology, quantum physics, computation and evolution.
All knowledge creation is a three-step process: meeting a problem, guessing a solution, and then, criticizing it. This is true for art, philosophy and math.
Since knowledge grows through criticism, we can never claim 100% certainty, as we don’t justify or create positive evidence for theories (even in mathematics).
Science wants to understand the world, which inescapably means explaining it. Prediction is a mean for criticizing theories, not an end on its own.
Explanations can’t be reduced to fundamental particles, for that is not an explanation at all. Good explanations invoke abstract and emergent phenomena.
Knowledge grows both in breadth (number of theories) and depth (scope of theories), the second one is winning. Thus, in the long-run all our theories will converge to one, that would be the theory of everything. It won’t be reductive, for good explanations invoke abstract and emergent phenomena. It also won’t be our last theory, since knowledge grows through criticism, not justification.
As we irreducibly use physical and abstract phenomena in our explanations, they both exist. For whether something is real or not depends on whether it is in our best explanations of the world.
Physical world provides a narrow window through which we observe the world of abstractions. Together they form the reality we are in.
Knowledge is a physical force, it can transform the landscape of Earth, and much more.
The only true constraints are laws of physics.
Everything they allow is achievable, the question is: How?
Knowledge is the answer.
Are things that create knowledge significant?
Their significance depends on knowledge power. With the right knowledge one can bend the universe to their will. Thus, things that create knowledge are universally significant.
Thus, life and humans are universally significant.
Evolution and epistemology both rely on variation and selection. This is for a reason, as the defining characteristic of life is knowledge creation and knowledge embodiment.
To those that seek explanations, quantum physics implies one thing loud and clear — reality is far bigger than we ever imagined, it consists of an infinite number of parallel universes which together form a multiverse. Every fiction that doesn’t violate laws of physics is a fact in the multiverse.
Quantum physics unlocks a qualitatively better mode of computation — quantum computers. They calculate intractable things for classical computers, and one cannot explain how they work without invoking parallel universes.
Computation is the process of calculating outputs from inputs by following some rules. Thus, a tree is a computer: its inputs are air, soil, and sun, by following genetic rules it is computing its output — growth and eventual death. Universe is a computer too: its input is the Big Bang, from which, by following the laws of physics it is computing its inevitable end.
Turing proved there can be a computer that can simulate any other computer — Universal Turing Machine. Thus, it can simulate anything in the universe arbitrarily well.
Universal Turing Machine doesn’t violate laws of physics, so it is built somewhere in the multiverse. Thus, laws of physics mandate their own understanding. Laws of physics mandate a knower.
So what would it take for reality to be understood? For knower to exist?
Only a bold guess that reality is understandable, and a relentless perseverance to make it such, fueled by blood, sweat and tears; all while staring straight into the deadliest beast of all — parochial social misconceptions, and fighting, fighting back; for there will be a knower — why not you?
My Favorite Quotes
understanding does not depend on knowing a lot of facts as such, but on having the right concepts, explanations and theories. — page 3
Prediction - even perfect, universal prediction - is simply no substitute for explanation. — page 5
To say that prediction is the purpose of a scientific theory is to confuse means with ends. It is like saying that the purpose of a spaceship is to burn fuel. In fact, burning fuel is only one of many things a spaceship has to do to accomplish its real purpose, which is to transport its payload from one point in space to another. Passing experimental tests is only one of many things a theory has to do to achieve the real purpose of science, which is to explain the world. — page 7
In reality, though, what happens is nothing like that. — page 41
Do not complicate explanations beyond necessity, because if you do, the unnecessary complications themselves will remain unexplained. — page 78
The Turing principle
It is possible to build a virtual-reality generator whose repertoire includes every physically possible environment. — page 135
If the laws of physics as they apply to any physical object or process are to be comprehensible, they must be capable of being embodied in another physical object - the knower. It is also necessary that processes capable of creating such knowledge be physically possible. Such processes are called science. — page 135
the laws of physics may be said to mandate their own comprehensibility. — page 135
CRYPTO-INDUCTIVIST: Yes. Please excuse me for a few moments while I adjust my entire world-view. — page 159
Inductivism is indeed a disease. It makes one blind. — page 165
one cannot predict the future of the Sun without taking a position on the future of life on Earth, and in particular on the future of knowledge. The colour of the Sun ten billion years hence depends on gravity and radiation pressure, on convection and nucleosynthesis. It does not depend at all on the geology of Venus, the chemistry of Jupiter, or the pattern of craters on the Moon. But it does depend on what happens to intelligent life on the planet Earth. It depends on politics and economics and the outcomes of wars. It depends on what people do: what decisions they make, what problems they solve, what values they adopt, and on how they behave towards their children. — page 184
To those who still cling to a single-universe world-view, I issue this challenge: explain how Shor’s algorithm works. I do not merely mean predict that it will work, which is merely a matter of solving a few uncontroversial equations. I mean provide an explanation. When Shor’s algorithm has factorized a number, using 10^500 or so times the computational resources that can be seen to be present, where was the number factorized? There are only about 10^80 atoms in the entire visible universe, an utterly minuscule number compared with 10^500. So if the visible universe were the extent of physical reality, physical reality would not even remotely contain the resources required to factorize such a large number. Who did factorize it, then? How, and where, was the computation performed? — page 217
the fabric of physical reality provides us with a window on the world of abstractions. It is a very narrow window and gives us only a limited range of perspectives. — page 255
Necessary truth is merely the subject-matter of mathematics, not the reward we get for doing mathematics. — page 253
they violate a basic tenet of rationality - that good explanations are not to be discarded lightly. — page 331
In view of all the unifying ideas that I have discussed, such as quantum computation, evolutionary epistemology, and the multiverse conceptions of knowledge, free will and time, it seems clear to me that the present trend in our overall understanding of reality is just as I, as a child, hoped it would be. Our knowledge is becoming both broader and deeper, and, as I put it in Chapter 1, depth is winning. But I have claimed more than that in this book. I have been advocating a particular unified world-view based on the four strands: the quantum physics of the multiverse, Popperian epistemology, the Darwin-Dawkins theory of evolution and a strengthened version of Turing’s theory of universal computation. It seems to me that at the current state of our scientific knowledge, this is the ‘natural’ view to hold. It is the conservative view, the one that does not propose any startling change in our best fundamental explanations. Therefore it ought to be the prevailing view, the one against which proposed innovations are judged. That is the role I am advocating for it. I am not hoping to create a new orthodoxy; far from it. As I have said, I think it is time to move on. But we can move to better theories only if we take our best existing theories seriously, as explanations of the world. — page 366
Find more quotes under the footnote.1
Found Mistakes?
This handbook will always be a work-in-progress. Yet, from now on I expect most of the future improvements to come from you — readers.
If you: find any mistakes, or have a better phrasing, or have a better example, or can think of any other improvement: comment below and I will update the handbook!
The beauty of internet as a medium is that you can easily correct and improve things. I want this handbook to stand the test of time, and become a timeless resources for all who are learning ideas of David.
Comment your proposals, I’ll review them all!
My Book Review
My goal for the first three month of the Self-Education year was to establish firm knowledge foundation. I couldn’t hope for a better companion than The Fabric of Reality. If you want to change the world you first must understand it, and this book is a great starting point.
For someone who spend 400 hours on it I won’t say something unexpected. Obviously this is a masterpiece, obviously this is the best book I’ve ever read on par with The Beginning of Infinity.
It changed me as a person.
It demystified the world.
It revealed interesting questions.
I’ve changed my life, my expectations and my desires to pursue some of them.
David brought so much value to me that I had to give something back. This is my attempt.
⭕ 1 — The Theory of Everything
It seems impossible for someone to know everything that is known nowadays, but is that so? Only if one believes it is about memorizing facts. Knowledge is a matter of understanding. It relies on good explanations, not myriad of facts. Good explanations are hard to come by, which is for the best for only a few must be taken seriously.
In this chapter David refutes instrumentalism and reductionism. He outlines an important thesis of the book: knowledge grows both in depth and breadth, but depth is winning. Thus, eventually one theory will encompass everything we know, from math to psychology. That would be The Theory of Everything.
1.1 On fallibility:
This would not be our last discovery, for our knowledge is fallible and we will always improve upon it. It will be one of the first such theories.
Summary
{I rarely use David’s chapter summaries, but this one is great.}
Scientific knowledge, like all human knowledge, consists primarily of explanations. Mere facts can be looked up, and predictions are important only for conducting crucial experimental tests to discriminate between competing scientific theories that have already passed the test of being good explanations. As new theories supersede old ones, our knowledge is becoming both broader (as new subjects are created) and deeper (as our fundamental theories explain more, and become more general). Depth is winning. Thus we are not heading away from a state in which one person could understand everything that was understood, but towards it. Our deepest theories are becoming so integrated with one another that they can be understood only jointly, as a single theory of a unified fabric of reality. This Theory of Everything has a far wider scope than the ‘theory of everything’ that elementary particle physicists are seeking, because the fabric of reality does not consist only of reductionist ingredients such as space, time and subatomic particles, but also, for example, of life, thought and computation. The four main strands of explanation which may constitute the first Theory of Everything are:
quantum physics Chapters 2, 9, 1 1, 12, 13, 14
epistemology Chapters 3, 4, 7, 10, 13, 14
the theory of computation Chapters 5, 6, 9, 10, 13, 14
the theory of evolution Chapters 8, 13, 14
— Page 30
You can practice chapter questions as flashcards here.
Understanding and Scientific Theories
1.1.0 What composes understanding? Explain on planetary motions.
Being able to predict, how ever accurate, does not equal understanding. One can memorize the archives and make ‘accurate’ predictions. Does it mean one understands planetary motions? No. One can memorize the formula and make accurate predictions of infinitely more scenarios. Does a higher number of accurate predictions equal understanding? No.
Planetary motions are understood when they are explained. Good theories have deep explanations and accurate predictions in one.
understanding does not depend on knowing a lot of facts as such, but on having the right concepts, explanations and theories. …
Being able to predict things or to describe them, however accurately, is not at all the same thing as understanding them. …
even though the formula summarizes infinitely more facts than the archives do, knowing it does not amount to understanding planetary motions. Facts cannot be understood just by being summarized in a formula, any more than by being listed on paper or committed to memory. They can be understood only by being explained. Fortunately, our best theories embody deep explanations as well as accurate predictions. For example, the general theory of relativity explains gravity in terms of a new, four-dimensional geometry of curved space and time. It explains precisely how this geometry affects and is affected by matter. That explanation is the entire content of the theory; predictions about planetary motions are merely some of the consequences that we can deduce from the explanation. —page 3
1.1.1 What is an explanation?
We all intuitively know, but defining it precisely is hard. It is about the why, not what and it seems to be a unique function of a human brain.
Roughly speaking, they are about ‘why’ rather than ‘what’; about the inner workings of things; about how things really are, not just how they appear to be; about what must be so, rather than what merely happens to be so; about laws of nature rather than rules of thumb. They are also about coherence, elegance and simplicity, as opposed to arbitrariness and complexity, though none of those things is easy to define either. — page 11
1.2.0 What are the three most valuable attributes of a scientific theory?
First, it explains an underlying truth that we cannot experience directly. Science explains seen in terms of unseen. Earth’s mass and curvature of spacetime explains why apple falls.
Second, scientific theories have both explanatory and predictive power, with the former we change the world. General relativity’s explanation of spacetime helps us to build spaceships and GPS navigation.
Third, a good scientific theory has a universal reach — beyond what is currently known. General relativity entirely explains quasars, yet they were discovered only 30 years after Einstein’s work. [1.1]
Similarly, when I say that I understand how the curvature of space and time affects the motions of planets, even in other solar systems I may never have heard of, I am not claiming that I can call to mind, without further thought, the explanation of every detail of the loops and wobbles of any planetary orbit. What I mean is that I understand the theory that contains all those explanations, and that I could therefore produce any of them in due course, given some facts about a particular planet. Having done so, I should be able to say in retrospect, ‘Yes, I see nothing in the motion of that planet, other than mere facts, which is not explained by the general theory of relativity.’ We understand the fabric of reality only by understanding theories that explain it. And since they explain more than we are immediately aware of, we can understand more than we are immediately aware that we understand. — page 12
1.3.0 Where are usually the main improvements between successive theory? Explain on general relativity and Newtonian physics.
The main difference with successive theory lies in explanations. General relativity’s predictions of planetary motions is a shade better than Newton’s theory, yet its explanatory power is unrivaled. Better explanations unlock creation of previously inaccessible technologies, like [GPS navigation](https://www.gpsworld.com/inside-the-box-gps-and-relativity/#:~:text=Advances in space-qualified atomic,nanosecond level to its users.).
1.2 On predictive power.
Don’t underestimate improvement in predictive power: general relativity predictions of black holes behavior is significantly better than Newtonian physics. [1.2]
the general theory of relativity explains gravity in terms of a new, four-dimensional geometry of curved space and time. It explains precisely how this geometry affects and is affected by matter. That explanation is the entire content of the theory; predictions about planetary motions are merely some of the consequences that we can deduce from the explanation.
What makes the general theory of relativity so important is not that it can predict planetary motions a shade more accurately than Newton’s theory can, but that it reveals and explains previously unsuspected aspects of reality, such as the curvature of space and time. — page 3
Instrumentalism and Reductionism
1.4.0 What is instrumentalism?
The view that the basic purpose of science is to predict an experiment, not to explain the reality. Explanations for instrumentalists are no more than psychological props — empty words.
The important thing is to be able to make predictions about images on the astronomers’ photographic plates, frequencies of spectral lines, and so on, and it simply doesn’t matter whether we ascribe these predictions to the physical effects of gravitational fields on the motion of planets and photons [as in pre-Einsteinian physics] or to a curvature of space and time. — Gravitation and Cosmology, page 147
1.4.1 What is the criticism of instrumentalism?
Science aims to understand reality, not merely predict it. Imagine we are given an oracle that can predict an outcome of any experiment but provides no explanation. For instrumentalists, science would be over!
First, we would be interested in how an oracle works. Second, how would it help us to build a better spaceship? Oracle could be used to test our design, not create it. If it fails it wouldn’t tell us why, just as with physical world. The **oracle is no different, it would only save us time and expenses on building a spaceship. Explaining the failure and improving the design would be on us, it would require understanding.
1.3 On predicting a fair roulette.
One can also consider a fair roulette. It would be impossible to predict, but does it mean that science can’t understand it? Certainly not. With good explanation one can understand why predicting a fair roulette is impossible.
Prediction - even perfect, universal prediction - is simply no substitute for explanation. — page 5
1.4.2 If wrong, why instrumentalism is so popular in academia?
It sounds superficially plausible because prediction is required to refute theories. It is a necessary part of the scientific method, but not its goal.
To say that the purpose of science is to make predictions is to confuse means with ends. Is the purpose of a spaceship to burn fuel? It is not. Its purpose is to travel from point A to point B and carry some load. The purpose of science is to explain the world and we do so by testing predictions of our most promising theories. {Want to remind yourself what is the scientific method? Review card 3.3.1}
although prediction is not the purpose of science, it is part of the characteristic method of science. The scientific method involves postulating a new theory to explain some class of phenomena and then performing a crucial experimental test, an experiment for which the old theory predicts one observable outcome and the new theory another. One then rejects the theory whose predictions turn out to be false. Thus the outcome of a crucial experimental test to decide between two theories does depend on the theories’ predictions, and not directly on their explanations. This is the source of the misconception that there is nothing more to a scientific theory than its predictions. — page 6
1.5.0 We reject theories by testing their predictions. Is this the only process by which we can grow scientific knowledge?
No. Many theories are rejected because they have bad explanations. Consider a theory that eating a kilo of grass will cure a common cold. This theory never gets to the experimental testing phase because it has no good explanation in the first place, so we never bother to test it.
1.5 On good explanations.
In The Beginning of Infinity David introduces a criterion for rejecting theories alike: bad theories have explanations that are easy to vary. Refer to The Beginning of Infinity, page 22.
experimental testing is by no means the only process involved in the growth of scientific knowledge. The overwhelming majority of theories are rejected because they contain bad explanations, not because they fail experimental tests. We reject them without ever bothering to test them. For example, consider the theory that eating a kilogram of grass is a cure for the common cold. That theory makes experimentally testable predictions: if people tried the grass cure and found it ineffective, the theory would be proved false. But it has never been tested and probably never will be, because it contains no explanation - either of how the cure would work, or of anything else. — page 7
1.6.0 What is reductionism?
The view that science always explains things reductively — analyzing them into smaller components and appealing to past events as causes.
1.6.1 What is the criticism of reductionism?
First, it disregards emergence — sometimes low-level complexity yields high-level simplicity. For instance a cat is easier to predict and explain, than an interaction of trillions of atoms.
Second, it believes that knowledge is always created by breaking down things into smaller components. However, this is false, we frequently understand things by appealing to high-level sciences.
Let’s consider a particular copper atom at the tip of the nose of Winston Churchill’s statue in London. Why is it there? Breaking down the statue to its subatomic particles and trying to explain their position by previous particle interactions only leads to an infinite regress. Eventually we would arrive at the Big Bang, yet, we would still have no explanation or understanding of why that copper atom is there. Nonetheless, if we appeal to history and culture (emergent phenomena) the why is rather obvious:
It is because Churchill served as prime minister in the House of Commons nearby; and because his ideas and leadership contributed to the Allied victory in the Second World War; and because it is customary to honour such people by putting up statues of them; and because bronze, a traditional material for such statues, contains copper, and so on. — page 22
{1.6 For more details watch this.}
Third, reductionism assumes that knowledge is always created by appealing to earlier events (i.e. stating causes). Yet, this is false even in fundamental physics! How could we know so much about the initial state of the universe if we have no idea of what was before it? How could we understand the time so well?! What was before it?
The Theory of Everything
1.7.0 What is the structure of science?
Reductionism assumes that low-level sciences are more important than high-level ones, but that is false. They both help us to understand and explain the world. One should search and accept a good explanation regardless of its scientific level. [1.3]
1.8.0 What David means by the Theory of Everything?
David believes that eventually our explanations of the world will converge to a single theory of everything that is understood by us. It would contain every known subject: math, physics, epistemology, history and so on. It won’t be reductive, as explanations can be found on many levels of reality.
The Theory of Everything would not encompass everything there is. Our knowledge is fallible, thus we’ll never approach this ideal (This is why David’s last book is called The Beginning of Infinity!). Hence, it also won’t be our last theory, for we will always be wrong and improve upon it.
1.8.1 Why will knowledge eventually converge to a single theory?
Knowledge is growing both in depth and breadth. Yet, with the accumulation of theories many render their usefulness and are replaced by singular deeper explanations. In the long run, those will converge to and we will have a unified theory of reality.
So, even though our stock of known theories is indeed snow balling, just as our stock of recorded facts is, that still does not necessarily make the whole structure harder to understand than it used to be. For while our specific theories are becoming more numerous and more detailed, they are continually being ‘demoted’ as the understanding they contain is taken over by deep, general theories. And those theories are becoming fewer, deeper and more general. By ‘more general’ I mean that each of them says more, about a wider range of situations, than several distinct theories did previously. By ‘deeper’ I mean that each of them explains more embodies more understanding - than its predecessors did, combined. — page 13
Consider building a house or a cathedral. Centuries ago we would require multiple master builders that have studied for decades to acquire general rules of thumb and intuitions. Each of them would be highly specialized, applying their skills to even slightly different problems would yield hopelessly wrong answers. Nonetheless, any architect nowadays studies not only less, but also can solve wide ranging problems, for he is relying on deep theories of reality, which are universally applicable.
Progress to our current state of knowledge was not achieved by accumulating more theories of the same kind as the master builder knew. Our knowledge, both explicit and inexplicit, is not only much greater than his but structurally different too. As I have said, the modern theories are fewer, more general and deeper. For each situation that the master builder faced while building something in his repertoire - say, when deciding how thick to make a load bearing wall - he had a fairly specific intuition or rule of thumb, which, however, could give hopelessly wrong answers if applied to novel situations. Today one deduces such things from a theory that is general enough for it to be applied to walls made of any material, in all situations: on the Moon, underwater, or wherever. The reason why it is so general is that it is based on quite deep explanations of how materials and structures work. …
That is why, despite understanding incomparably more than an ancient master builder did, a modern architect does not require a longer or more arduous training. A typical theory in a modern student’s syllabus may be harder to understand than any of the master builder’s rules of thumb; but the modern theories are far fewer, and their explanatory power gives them other properties such as beauty, inner logic and connections with other subjects which make them easier to learn. Some of the ancient rules of thumb are now known to be erroneous, while others are known to be true, or to be good approximations to the truth, and we know why that is so. A few are still in use. But none of them is any longer the source of anyone’s understanding of what makes structures stand up. — page 14
1.8.2 What this implies?
More knowledge does not equal more theories. This grand unification will make it only more feasible to understand everything that is understood.
Our best theories might be harder to understand than rules of thumb, but this is not a significant barrier. Theory’s depth has no correlation with its complexity, in fact, frequently consolidation makes it only easier to understand. Consider electromagnetism:
a new theory may be a unification of two old ones, giving us more understanding than using the old ones side by side, as happened when Michael Faraday and James Clerk Maxwell unified the theories of electricity and magnetism into a single theory of electromagnetism. More indirectly, better explanations in any subject tend to improve the techniques, concepts and language with which we are trying to understand other subjects, and so our knowledge as a whole, while increasing, can become structurally more amenable to being understood. — page 9
🎞️ 2 — Shadows
In this chapter David explains the basis of quantum physics — an experiment from which we infer there are parallel universes (and why physicist refer to it as a multiverse). This conclusion is accessible to those that seek explanations, not predictions.
Summary
Light is made out of smallest discrete particles called photons. In fact, quantum physics states that all matter is made out of smallest inseparable particles.
Does light travel in straight lines only? On a bigger scale it does, for we cannot see around the corners, but when constrained to smaller sizes it bends.
If you put two slits and shed light from them you’ll get an unusual striped shadows.
It’s weird, but not disturbing since we know that light bends on a smaller scale. We can explain the shadows by saying that photons bump with each other like billiard balls, interfering and producing the pattern.
What would happen if we send just one photon? The disturbing part is that with enough time we’ll get exactly the same pattern. But what could be interfering? We can put detector on each slit that goes off whenever a photon is passing by. Maybe our single photon splits and interfere with itself.
Yet, we always observe only one slit going off. So nothing detectable is passing through the other slits, and yet if close them we’ll get a different pattern. So something is passing through! We quickly find out that whatever is passing also behaves like light — it penetrates diamond, but not fog.
Such results repeat for every other element, not just light. To explain the interference of a singular photon we must say that there are additional ‘shadow’ photons travelling with it that we can’t see, yet they impact the one we can see. As the same is true for elements, we say there are additional ‘shadow’ elements for every one that is visible to us. Elements and photons, together form a universe. A parallel universe.
You can practice chapter questions as flashcards here.
Properties of Light
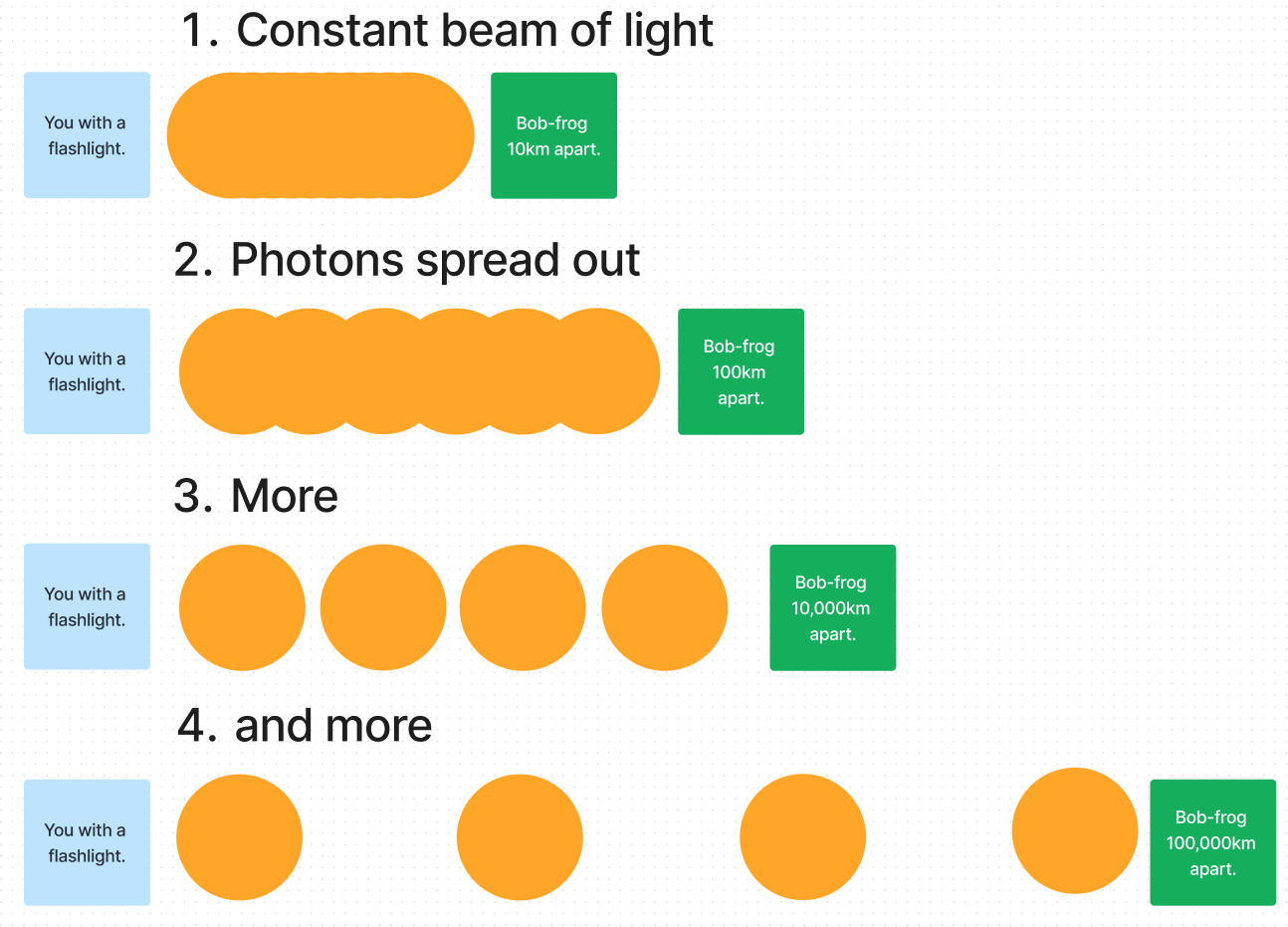
2.1.0 Imagine an infinite empty room with no light. What would you see if you turned on a flashlight in your hand?
Nothing; if light has no matter to reflect upon, it won’t arrive in your eye!
2.2.0 Let’s imagine there is someone 10km away from you — we’ll call him Bob. If you were to turn on the flashlight, is there a distance from which Bob would entirely lose sight of light?
There isn’t! Regardless of how far he walks away he would see light.
2.2.1 What exactly would he see?
This requires a more detailed answer! First, I must confess, eventually Bob would lose sight because human eyes are not that sensitive to light. Nonetheless, if we turn Bob into a frog, than his eyes would be just right to always see light.
2.2.2 Would he see a constant stream of light?
This question highlights the fundamental difference between classical and quantum physics.
In classical physics matter is continuous — regardless of how much you ‘zoom-in’ you will never get to the smallest lump of something. Hence, there will always be a constant beam of light that never seizes to zero, yet the further you go, the tinier it gets. Thus, in classical physics you can spread light ever more thinly without a limit. Same holds for matter, a sheet of gold could be spread thinner and thinner without an end.
In quantum physics it is the other way around. Quantum literally means the smallest lump of something. Everything can be broken down into the smallest parts, but no smaller, and hence, everything (both light and matter) appear in chunks of discrete sizes.
2.2.3 So what would Bob-frog see?
Quantum physics states that light is made out of the smallest discrete units — photons. So once Bob-frog gets far enough, he won’t see a constant beam, he would see a flickering of photons. The further he goes, the more periodic they are. But brightness would stay the same, as it is always one photon!
The photons stay the same, yet as you move away their frequency decreases:
Not to scale!
The same idea applies for a sheet of gold:
the only way in which one can make a one-atom-thick gold sheet even thinner is to space the atoms farther apart, with empty space between them. When they are sufficiently far apart it becomes misleading to think of them as forming a continuous sheet. For example, if each gold atom were on average several centimetres from its nearest neighbour, one might pass one’s hand through the ‘sheet’ without touching any gold at all. Similarly, there is an ultimate lump or ‘atom’ of light, a photon. Each flicker seen by the frog is caused by a photon striking the retina of its eye. …
When the beam is very faint it can be misleading to call it a ‘beam’, for it is not continuous. During periods when the frog sees nothing it is not because the light entering its eye is too weak to affect the retina, but because no light has entered its eye at all. — page 35
2.3.0 What is the quantization property?
The property of matter and light appearing only in lumps of discrete sizes. A single lump (like a photon) is called quantum.
This property of appearing only in lumps of discrete sizes is called quantization. An individual lump, such as a photon, is called a quantum (plural quanta). Quantum theory gets its name from this property, which it attributes to all measurable physical quantities - not just to things like the amount of light, or the mass of gold, which are quantized because the entities concerned, though apparently continuous, are really made of particles. — page 35
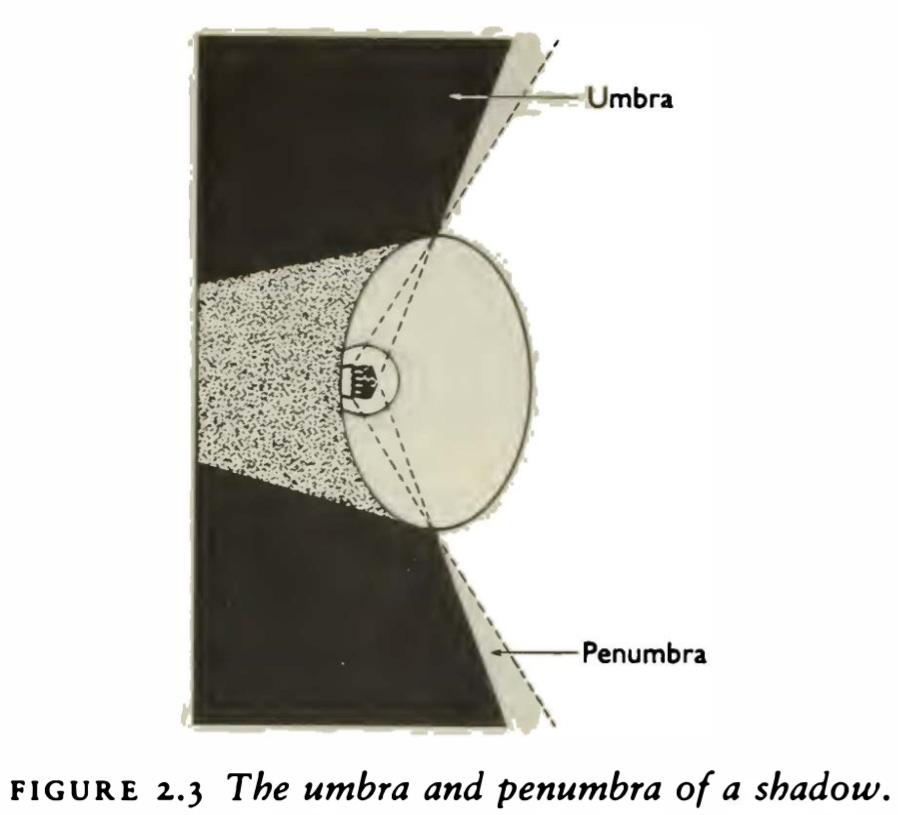
2.4.0 Our next two questions are directly taken from the book. Consider this picture:
is there, in principle, any limit on how sharp a shadow can be (in other words, on how narrow a penumbra can be)? For instance, if the torch were made of perfectly black (non-reflecting) material, and if one were to use smaller and smaller filaments, could one then make the penumbra narrower and narrower, without limit? — page 36
2.4.0 Answer
Penumbra can get narrower only if light always travels in straight lines. In our daily life’s it does — for we cannot see around the corners! Yet, when confined to small sizes — it rebels.
2.4.1 Consider this picture:
if the experiment is repeated with ever smaller holes and with ever greater separation between the first and second screens, can one bring the umbra - the region of total darkness - ever closer, without limit, to the straight line through the centres of the two holes? Can the illuminated region between the second and third screens be confined to an arbitrarily narrow cone? — page 37
2.4.1 Answer
It cannot! The result is illustrated in the figure 2.5:
even with holes as large as a millimetre or so in diameter, the light begins noticeably to rebel. Instead of passing through the holes in straight lines, it refuses to be confined and spreads out after each hole. And as it spreads, it ‘frays’. The smaller the hole is, the more the light spreads out from its straight-line path. Intricate patterns of light and shadow appear. We no longer see simply a bright region and a dark region on the third screen, with a penumbra in between, but instead concentric rings of varying thickness and brightness. — page 38
When confined to small sizes light frays and bends; you might ask: “So what? It may be interesting, but fundamentally, it’s not disturbing”. And I agree, so let’s get to the disturbing part ;)
Double Slit Experiment
2.5.0 Imagine an opaque barrier that has two straight, parallel slits which are separated by 0.2 millimetres apart:
If we shed light through the slights we get unusual shadows, but they just verify our past conclusion (that light ‘rebels’ when constrained to small sizes):
Now, what sort of shadow is cast if we cut a second, identical pair of slits in the barrier, interleaved with the existing pair, so that we have four slits at intervals of one-tenth of a millimetre? — page 40
2.5.0 Answer
We might expect the pattern to look almost exactly like Figure 2.6. After all, the first pair of slits, by itself, casts the shadows in Figure 2.6, and as I have just said, the second pair, by itself, would cast the same pattern, shifted about a tenth of a millimetre to the side - in almost the same place. We even know that light beams normally pass through each other unaffected. So the two pairs of slits together should give essentially the same pattern again, though twice as bright and slightly more blurred.
In reality, though, what happens is nothing like that. — page 41
Figure 2.7 illustrates what happens, adding two more slides somehow darkens the point X:
2.5.1 What are possible explanations for this phenomena?
David proposes:
One might imagine two photons heading towards X and bouncing off each other like billiard balls. Either photon alone would have hit X, but the two together interfere with each other so that they both end up elsewhere. I shall show in a moment that this explanation cannot be true. Nevertheless, the basic idea of it is inescapable: something must be coming through that second pair of slits to prevent the light from the first pair from reaching X. But what? We can find out with the help of some further experiments. — page 41
We establish that whatever interferes with the shadows behaves like light:
First, the four-slit pattern of Figure 2.7(a) appears only if all four slits are illuminated by the laser beam. If only two of them are illuminated, a two-slit pattern appears. If three are illuminated, a three-slit pattern appears, which looks different again. So whatever causes the interference is in the light beam. The two-slit pattern also reappears if two of the slits are filled by anything opaque, but not if they are filled by anything transparent. In other words, the interfering entity is obstructed by anything that obstructs light, even something as insubstantial as fog. But it can penetrate anything that allows light to pass, even something as impenetrable (to matter) as diamond. If complicated systems of mirrors and lenses are placed anywhere in the apparatus, so long as light can travel from each slit to a particular point on the screen, what will be observed at that point will be part of a four-slit pattern. — page 42
2.5.2 What would then happen if we fire just one photon through two and four slits?
Interference is caused by something that behaves like a photon, hence, if we send just one it won’t happen. We might expect some new pattern to emerge, but what we should not see is some place on the screen (like X) that goes dark when two additional slits are opened (for that is an interference).
Yet. This is exactly what we observe.
Even when the experiment is done with one photon at a time, none of them is ever observed to arrive at X when all four slits are open. Yet we need only close two slits for the flickering at X to resume. — page 43
2.5.3 “Could it be that the photon splits into fragments which, after passing through the slits, change course and recombine?”— page 43
We can rule that possibility out too. If, again, we fire one photon through the apparatus, but use four detectors, one at each slit, then at most one of them ever registers anything. Since in such an experiment we never observe two of the detecters going off at once, we can tell that the entities that they detect are not splitting up. So, if the photons do not split into fragments, and are not being deflected by other photons, what does deflect them? When a single photon at a time is passing through the apparatus, what can becoming through the other slits to interfere with it? — page 43
2.5.4 Let’s revisit our findings so far.
We have found that when one photon passes through this apparatus,
it passes through one of the slits, and then something interferes with it,
deflecting it in a way that depends on what other slits are open;
the interfering entities have passed through some of the other slits;
the interfering entities behave exactly like photons ...
. . . except that they cannot be seen. — page 43
2.5.5 What can we infer from this?
Whatever interferences with our photon, behaves also like a photon, but we can’t detect it. For now, we’ll refer to it as ‘shadow photons’.
I shall now start calling the interfering entities ‘photons’. That is what they are, though for the moment it does appear that photons come in two sorts, which I shall temporarily call tangible photons and shadow photons. Tangible photons are the ones we can see, or detect with instruments, whereas the shadow photons are intangible (invisible) - detectable only indirectly through their interference effects on the tangible photons. — page 43
2.5.6 How many shadow photons accompany a tangible one?
The Fabric of Reality was published in 1997 and the lower bound was at one trillion shadow photons.
2.3 On number of universes.
It is either very very large number of infinite. Once you study the Multiverse chapter of The Beginning of Infinity you realize how this question seizes its meaning. There are no actual universes in our classical meaning of the word. It is one extremely large multiverse, that subjectively appears to consist of independent universes, but it’s all part of one structure.
Since different interference patterns appear when we cut slits at other places in the screen, provided that they are within the beam, shadow photons must be arriving all over the illuminated part of the screen whenever a tangible photon arrives. Therefore there are many more shadow photons than tangible ones. How many? Experiments cannot put an upper bound on the number, but they do set a rough lower bound. In a laboratory the largest area that we could conveniently illuminate with a laser might be about a square metre, and the smallest manageable size for the holes might be about a thousandth of a millimetre. So there are about 10^12 (one trillion) possible hole-locations on the screen. Therefore there must be at least a trillion shadow photons accompanying each tangible one. — page 44
2.5.7 Is the interference effect limited to photons only?
No, similar phenomena occur in every type of particle.
2.5.8 Considering our discussion above, what conclusion it implies?
there must be hosts of shadow neutrons accompanying every tangible neutron, hosts of shadow electrons accompanying every electron, and so on. Each of these shadow particles is detectable only indirectly, through its interference with the motion of its tangible counterpart.
It follows that reality is a much bigger thing than it seems, and most of it is invisible. The objects and events that we and our instruments can directly observe are the merest tip of the iceberg.
Now, tangible particles have a property that entitles us to call them, collectively, a universe. This is simply their defining property of being tangible, that is, of interacting with each other, and hence of being directly detectable by instruments and sense organs made of other tangible particles. Because of the phenomenon of interference, they are not wholly partitioned off from the rest of reality (that is, from the shadow particles). If they were, we should never have discovered that there is more to reality than tangible particles. But to a good approximation they do resemble the universe that we see around us in everyday life, and the universe referred to in classical (pre-quantum) physics. — page 44
2.5.9 So far we have inferred an existence of a ‘shadow universe’ which seems to be at least trillion times bigger than ours. How then, do we know that these shadow particles are actually grouped into parallel universes like ours?
We start with the fact that a tangible barrier is not influenced by a shadow photon. If we put a detector it never goes off, so the shadow photon can’t be stopped by it.
To put that another way, shadow photons and tangible photons are affected in identical ways when they reach a given barrier, but the barrier itself is not identically affected by the two types of photon. — page 46
What stops the shadow photon then? If it was anything from tangible atoms we could sense it. We know that every kind of particle has a shadow counterpart, thus it seems that shadow photons are stopped by shadow atoms (i.e. shadow barriers).
this shadow barrier is made up of the shadow atoms that we already know must be present as counterparts of the tangible atoms in the barrier. There are very many of them present for each tangible atom. Indeed, the total density of shadow atoms in even the lightest fog would be more than sufficient to stop a tank, let alone a photon, if they could all affect it. Since we find that partially transparent barriers have the same degree of transparency for shadow photons as for tangible ones, it follows that not all the shadow atoms in the path of a particular shadow photon can be involved in blocking its passage. Each shadow photon encounters much the same sort of barrier as its tangible counterpart does, a barrier consisting of only a tiny proportion of all the shadow atoms that are present.
For the same reason, each shadow atom in the barrier can be interacting with only a small proportion of the other shadow atoms in its vicinity, and the ones it does interact with form a barrier much like the tangible one. And so on. All matter, and all physical processes, have this structure. …
In other words, particles are grouped into parallel universes. They are ‘parallel’ in the sense that within each universe particles interact with each other just as they do in the tangible universe, but each universe affects the others only weakly, through interference phenomena. — page 46
2.6.0 In our explanations of parallel universes we have the idea of tangible universe and shadow universes. What exactly differentiates them?
Only its subjective point of view. Let’s come back to the example at the start of the chapter with our Bob-frog and a flashlight in an infinitely big dark room. We now know there are at least a trillion shadow universes with exactly the same Bob-frogs and flashlights as in our ‘tangible’ universe. But for them, their universe is tangible and ours is shadow. There is no inherent difference between the universes, just the subjective point of view.
Let’s also say that we asked Bob-frog to jump once he sees the flickering. Before we turn on a flashlight all universes are identical. Yet the precise time of its arrival varies, so the multiverse will start splitting depending on a photon and Bob-frog’s jump.
While I was writing that, hosts of shadow Davids were writing it too. They too drew a distinction between tangible and shadow photons; but the photons they called ‘shadow’ include the ones I called ‘tangible’, and the photons they called ‘tangible’ are among those I called ‘shadow’.
Not only do none of the copies of an object have any privileged position in the explanation of shadows chat I have just outlined, neither do they have a privileged position in the full mathematical explanation provided by quantum theory. I may feel subjectively that I am distinguished among the copies as the ‘tangible’ one, because I can directly perceive myself and not the others, but I must come to terms with the fact that all the others feel the same about themselves.
Many of those Davids are at this moment writing these very words. Some are putting it better. Others have gone for a cup of tea. — page 53
🔓 3 — Problem-solving
Claiming the existence of parallel universes is a radical world-view from any perspective. How do we know? How do we arrive at such conclusions? These questions are studied under epistemology — the main focus of this chapter.
David explains why inductivism is false, and what the true process of science is — Popperian epistemology. He also touches upon solipsism, which we’ll discuss in detail next time.
Summary
Empiricism is a philosophical view that we derive knowledge from our senses. It is wrong for it doesn’t explain how we choose what to observe, there are infinite things to look at, we can’t observe all at once.
Solipsism is a set of philosophical theories that say reality has some boundary, like matrix, or that it’s all a dream happening in your head.
Induction says that knowledge is created by pure observation and extrapolation of those observations. Observation can’t be pure for it is a mistake of empiricism. But the other problem is that it tries to justify theories by doing more observations. This is bad, for the same observation can ‘justify’ diametrically opposite theories.
Popperian epistemology comes to replace both empiricism and induction. It says that all knowledge creation is about problem-solving. You guess a solution to the problem and then criticize it, not try to prove it right.
Moreover, all our observations are based on our theories, so that solves the empiricism problem. Finally, since all knowledge is just a guess, and observations are based on theories (that can be wrong) — all our knowledge is fallible. We can never have a 100% certainty about anything, even that 2+2 is 4, for we use our brain that is fallible. Popper claims we never create a positive evidence for theory (like in induction), we can only criticize it.
You can practice chapter questions as flashcards here.
Empiricism, Solipsism and Induction
3.1.0 What is empiricism? What is its criticism?
Empiricism is a philosophical view that we derive knowledge from our senses. It is wrong for it doesn’t explain how out of infinite possible things to pay attention to, we choose one over the other. We must rely on something, it can’t be just pure observation, as there is too much to observe.
we do not directly perceive the stars, spots on photographic plates, or any other external objects or events. We see things only when images of them appear on our retinas, and we do not perceive even those images until they have given rise to electrical impulses in our nerves, and those impulses have been received and interpreted by our brains. Thus the physical evidence that directly sways us, and causes us to adopt one theory or world-view rather than another, is less than millimetric: it is measured in thousandths of a millimetre (the separation of nerve fibres in the optic nerve), and in hundredths of a volt (the change in electric potential in our nerves that makes the difference between our perceiving one thing and perceiving another). …
however sophisticated the instruments we use, and however substantial the external causes to which we attribute their readings, we perceive those readings exclusively through our own sense organs. There is no getting away from the fact that we human beings are small creatures with only a few inaccurate, incomplete channels through which we receive all information from outside ourselves. We interpret this information as evidence of a large and complex external universe (or multiverse). But when we are weighing up this evidence, we are literally contemplating nothing more than patterns of weak electric current trickling through our own brains.
What justifies the inferences we draw from these patterns? — page 57
3.2.0 What is solipsism?
Solipsism is a set of philosophical theories that claim that reality has some specific boundary. Some claim it is just a dream and nothing exist outside our mind, some claim the boundary around the Earth, our galaxy or matrix of some kind. This theories can be considered jointly because the ‘line’ is usually drawn arbitrarily, hence they can be refuted by the same means (which we’ll consider in the next chapter).
Solipsism, the theory that only one mind exists and that what appears to be external reality is only a dream taking place in that mind, cannot be logically disproved. Reality might consist of one person, presumably you, dreaming a lifetime’s experiences. Or it might consist of just you and me. Or just the planet Earth and its inhabitants. …
There is a large class of related theories here, but we can usefully regard them all as variants of solipsism. They differ in where they draw the boundary of reality (or the boundary of that part of reality which is comprehensible through problem-solving) , and they differ in whether, and how, they seek knowledge outside that boundary. But they all consider scientific rationality and other problem solving to be inapplicable outside the boundary - a mere game — page 58, 80
3.3.0 What is induction?
A philosophical view that knowledge creation happens by extrapolating or generalizing the results of observations.
3.3.1 What role observations play in this world-view?
In the inductivist theory of scientific knowledge, observations play two roles: first, in the discovery of scientific theories, and second, in their justification. A theory is supposed to be discovered by ‘extrapolating’ or ‘generalizing’ the results of observations. — page 59
3.3.2 What are the stages of inductivism? Describe the knowledge creation process on the shadows example from the past chapter.
if large numbers of observations conform to the theory, and none deviates from it, the theory is supposed to be justified - made more believable, probable or reliable. … The inductivist analysis of my discussion of shadows would therefore go something like this: ‘We make a series of observations of shadows, and see interference phenomena (stage 1). The results conform to what would be expected if there existed parallel universes which affect one another in certain ways. But at first no one notices this. Eventually (stage 2) someone forms the generalization that interference will always be observed under the given circumstances, and thereby induces the theory that parallel universes are responsible. With every further observation of interference (stage 3) we become a little more convinced of that theory. After a sufficiently long sequence of such observations, and provided that none of them ever contradicts the theory, we conclude (stage 4) that the theory is true. Although we can never be absolutely sure, we are for practical purposes convinced. — page 59
3.3.3. What is the criticism of induction? Describe an example of the Bertrand Russell chicken.
First, a generalized prediction is rarely a candidate for a new theory and our deepest theories seldom are generalizable. With the multiverse example we certainly have not observed first one universe, then second, then third, and then concluded there are trillions of them! {3.1 Induction and baby weight.}
Second, inductivism uses the same observations to ‘justify’ theories. Consider Russell’s chicken:
The chicken noticed that the farmer came every day to feed it. It predicted that the farmer would continue to bring food every day. Inductivists think that the chicken had ‘extrapolated’ its observations into a theory, and that each feeding time added justification to that theory. Then one day the farmer came and wrung the chicken’s neck. — page 60
Should the chicken believe that its feeding theory would become more certain (i.e. more justified) with each day (observation)? What if the chicken generalized a diametrically opposite theory? The same observations would then support it as well:
However, this line of criticism lets inductivism off far too lightly. It does illustrate the fact that repeated observations cannot justify theories, but in doing so it entirely misses (or rather, accepts) a more basic misconception: namely, that the inductive extrapolation of observations to form new theories is even possible. In fact, it is impossible to extrapolate observations unless one has already placed them within an explanatory framework. For example, in order to ‘induce’ its false prediction, Russell’s chicken must first have had in mind a false explanation of the farmer’s behaviour. Perhaps it guessed that the farmer harboured benevolent feelings towards chickens. Had it guessed a different explanation - that the farmer was trying to fatten the chickens up for slaughter, for instance - it would have ‘extrapolated’ the behaviour differently. Suppose that one day the farmer starts bringing the chickens more food than usual. How one extrapolates this new set of observations to predict the farmer’s future behaviour depends entirely on how one explains it. According to the benevolent-farmer theory, it is evidence that the farmer’s benevolence towards chickens has increased, and that therefore the chickens have even less to worry about than before. But according to the fattening-up theory, the behaviour is ominous - it is evidence that slaughter is imminent. — page 60
Depending on the chicken’s mood when farmer first time brought more food it would conclude that either it is about to die, or live a happy, long life. Induction provides no mechanism to distinguish theories.
Popperian Epistemology
3.4.0 What is the Popperian epistemology?
A philosophical theory that science is a problem-solving process. The problem arises when our current theories seem inadequate.
By a ‘problem’ I do not necessarily mean a practical emergency, or a source of anxiety. I just mean a set of ideas that seems inadequate and worth trying to improve. The existing explanation may seem too glib, or too laboured; it may seem unnecessarily narrow, or unrealistically ambitious. One may glimpse a possible unification with other ideas. Or a satisfactory explanation in one field may appear to be irreconcilable with an equally satisfactory explanation in another. Or it may be that there have been some surprising observations - such as the wandering of planets - which existing theories [celestial sphere] did not predict and cannot explain. — page 62
3.4.1 What are the stages of Popperian epistemology?
after a problem presents itself (stage 1), the next stage always involves conjecture: proposing new theories, or modifying or reinterpreting old ones, in the hope of solving the problem (stage 2). The conjectures are then criticized which, if the criticism is rational, entails examining and comparing them to see which offers the best explanations, according to the criteria inherent in the problem (stage 3). When a conjectured theory fails to survive criticism - that is, when it appears to offer worse explanations than other theories do - it is abandoned. If we find ourselves abandoning one of our originally held theories in favour of one of the newly proposed ones (stage 4), we tentatively deem our problem-solving enterprise to have made progress. I say ‘tentatively’, because subsequent problem solving will probably involve altering or replacing even these new, apparently satisfactory theories, and sometimes even resurrecting some of the apparently unsatisfactory ones. — page 64
3.2 On further inquiry.
If you’d like to dive-in further I recommend reading The Logic of Experimental Tests.
3.4.2 What fifth stage implies in the Popperian epistemology?
Popperian epistemology regards science as a never ending process, for our knowledge will always be fallible and improvable. Yet in induction we can arrive at the final truth, hence science has an end.
This difference is due to justification, **induction assumes that one can (or needs to) create positive evidence for a theory. But, if we just guess (conjecture) theories (solutions) then we are always fallible, for our senses and tools are so too. Our guesses are always approximations of reality, yet some are better than others, like general relativity and Newtonian physics.
Thus the solution, however good, is not the end of the story: it is a starting-point for the next problem-solving process (stage 5). This illustrates another of the misconceptions behind inductivism. In science the object of the exercise is not to find a theory that will, or is likely to, be deemed true for ever; it is to find the best theory available now, and if possible to improve on all available theories. A scientific argument is intended to persuade us that a given explanation is the best one available. — page 64
3.5.0 What is a crucial experimental test?
The distinguishing characteristic between scientific problem-solving is the use of experiments to rule out opposing theories (stage 3 in Popperian epistemology). How do we know that general relativity is better than Newtonian physics? We create an experiment where theories diverge in their predictions and then conduct it. Its outcome would refute one of the theories, so we conclude that the last man standing is our best explanation of reality, so far. It is a mistake to say that general relativity has been justified by the experiment, its outcome is just in-line with what the theory predicted. It doesn’t imply that the theory is the ultimate truth. In fact, theories can never be the ultimate truth, because they all are just our guesses, and we are fallible.
Scientific problem-solving always includes a particular method of rational criticism, namely experimental testing. Where two or more rival theories make conflicting predictions about the outcome of an experiment, the experiment is performed and the theory or theories that made false predictions are abandoned. The very construction of scientific conjectures is focused on finding explanations that have experimentally testable predictions. Ideally we are always seeking crucial experimental tests experiments whose outcomes, whatever they are, will falsify one or more of the contending theories. — page 65
3.6.0 What are the similarities between Popperian epistemology and evolution?
Both use error-correction mechanism: variation and selection in evolution, conjectures and refutations in epistemology. Be it scientific theories or genes, the essence of knowledge creation is in error-correction.
While a problem is still in the process of being solved we are dealing with a large, heterogeneous set of ideas, theories, and criteria, with many variants of each, all competing for survival. There is a continual turnover of theories as they are altered or replaced by new ones. So all the theories are being subjected to variation and selection, according to criteria which are themselves subject to variation and selection. The whole process resembles biological evolution. A problem is like an ecological niche, and a theory is like a gene or a species which is being tested for viability in that niche. Variants of theories, like genetic mutations, are continually being created, and less successful variants become extinct when more successful variants take over. ‘Success’ is the ability to survive repeatedly under the selective pressures - criticism - brought to bear in that niche, and the criteria for that criticism depend partly on the physical characteristics of the niche and partly on the attributes of other genes and species (i.e. other ideas) that are already present there. — page 67
3.6.1 What are the differences between Popperian epistemology and evolution?
One difference is that in biology variations (mutations) are random, blind and purposeless, while in human problem-solving the creation of new conjectures is itself a complex, knowledge-laden process driven by the intentions of the people concerned. Perhaps an even more important difference is that there is no biological equivalent of argument. All conjectures have to be tested experimentally, which is one reason why biological evolution is slower and less efficient by an astronomically large factor. Nevertheless, the link between the two sorts of process is far more than mere analogy: they are two of my four intimately related ‘main strands’ of explanation of the fabric of reality. — page 68
💤 4 — Criteria for Reality
When arguing for the multiverse world-view we have inexplicitly rejected a set of ‘solipsistic’ theories, while subscribing to realism. It is time to test that assumption.
Summary
Realism is the view that reality objectively exists, regardless of a subjective observer. Meaning, the chair you are sitting would still exists regardless of your looking at it or not.
Solipsism is the view that there is some boundary to reality, like that it is all a matrix, or a dream in your head. It is hard to disprove for every prediction it makes would also be in line with realism. So how do we distinguish the two?
Through a philosophical argument. Solipsism is wrong because it is easy to vary, it has one needless assumption that it’s all just a dream, or a matrix. This assumption is easy to vary, so we can fill-in the blank whatever we want, like: “It’s a matrix with two computers, not one! The second one running specifically for Chinese due to their firewall!”.
The same way we can distinguish between heliocentric (Earth moves around the Sun) and geocentric (everything moves around the Earth) theories. Geocentric theory make a needless assumption that is easy to vary, yet with heliocentric remove one note and harmony will fall.
Something is real or not if it is in our best explanations of reality.
You can practice chapter questions as flashcards here.
4.1.0 What is realism?
A view that reality objectively exists, regardless of any subjective observer. This means that the chair I am sitting on actually exists, and if I go to the cinema it would still exist, even though I won’t observe it. I don’t observe the computer you are reading this from, but your computer still exists.
The theory that an external physical universe exists objectively and affects us through our senses. — page 96
4.2.0 What makes solipsism hard to disprove?
Solipsism is problematic because one cannot empirically disprove it. Any observational evidence you collect is ‘in-line’ with the theory that you have dreamt it. So if you say that according to realism the ball should drop, then solipsism would say: “Just as you have said it, BUT! it’s all a dream (or matrix and so on).”. Any prediction you make, solipsism would make the same but with one additional assumption — it’s all just a dream (or matrix and so on). {Remind yourself what solipsism is in card 3.1.0}
[solipsism] cannot be logically disproved. Reality might consist of one person, presumably you, dreaming a lifetime’s experiences. Or it might consist of just you and me. Or just the planet Earth and its inhabitants. And if we dreamed evidence - any evidence - of the existence of other people, or other planets, or other universes, that would prove nothing about how many of those things there really are. — page 58
As we have mentioned solipsism is an umbrella term, for it could be used to describe a set of philosophies that make the same predictions as realism, but then draw an arbitrary boundary of existence (make just one more assumption). Instead of saying “it’s all just a dream”, some would say “it’s all just a matrix”, or reason has no value from here and on.
4.3.0 How can we disprove solipsism?
As we have shown, solipsism is immune to the experimental criticism — any observation is in-line with it. So how could we disprove it? {4.2 On hierarchy of criticisms. David explains that philosophical arguments are just as effective as experimental or mathematical ones. In fact, there is no hierarchy of proves, one should seek good explanations on any ‘level of sciences’; hopefully you remember this from the first chapter!}
We appeal to the philosophical argument! {4.3 On presented arguments. Important note: this is not the reason that David presents in the Fabric of Reality, we refute solipsism by his latest epistemological breakthrough of the ‘hard to vary’ criterion.}
The purpose of science is to understand the reality, we do so by explaining it. In science we search for good explanations. In his last book: The Beginning of Infinity, David makes an epistemological breakthrough by defining criterion for good explanations. Good explanations are hard to vary.
If we want to explain reality we have to be cautious with what we include in our explanations, one could rephrase Occam’s razor as:
Do not complicate explanations beyond necessity, because if you do, the unnecessary complications themselves will remain unexplained. — page 78
Hence our criticism of solipsism is twofold. First, the assumption that this is all just a dream has no good (hard to vary) explanation behind it, we just as successfully could say it is a matrix. Second, this additional assumption leaves more unexplained than explained: Where are you sleeping? How come you dream for so long? Why are you alive? Are the things that are not yet known to you, actually part of your brain (like quantum physics, or content of the next chapters 😉)? Same questions would apply to the matrix assumptions: Where is the computer? How it works? Who controls it? Can we escape it? Why they run it?
We have no observational evidence to conclude this is not a dream or matrix. But if we want to understand reality, we must search for hard to vary explanations. Any solipsism variation is just a realism with an additional assumption that is left unexplained and easily varied.
Thus solipsism, far from being a world-view stripped to its essentials, is actually just realism disguised and weighed down by additional unnecessary assumptions - worthless baggage, introduced only to be explained away. — page 83
4.4.0 What are the heliocentric and the geocentric theories?
heliocentric theory The theory that the Earth moves round the Sun, and spins on its own axis.
geocentric theory The theory that the Earth is at rest and other astronomical bodies move around it — page 96
David goes in great detail explaining the differences between the two in the book. The essence of it is:
The heliocentric theory explains them [planetary motions] by saying that the planets are seen to move in complicated loops across the sky because they are really moving in simple circles (or ellipses) in space, but the Earth is moving as well. The Inquisition’s explanation is that the planets are seen to move in complicated loops because they really are moving in complicated loops in space; but (and here, according to the Inquisition’s theory, comes the essence of the explanation) this complicated motion is governed by a simple underlying principle: namely, that the planets move in such a way that, when viewed from the Earth, they appear just as they would if they and the Earth were in simple orbits round the Sun.
To understand planetary motions in terms of the Inquisition’s theory, it is essential that one should understand this principle, for the constraints it imposes are the basis of every detailed explanation that one can make under the theory. For example, if one were asked why a planetary conjunction occurred on such-and-such a date, or why a planet backtracked across the sky in a loop of a particular shape, the answer would always be ‘because that is how it would look if the heliocentric theory were true’. So here is a cosmology - the Inquisition’s cosmology - that can be understood only in terms of a different cosmology, the heliocentric cosmology that it contradicts but faithfully mimics. — page 78
4.4.1 How do we choose between them?
Just as with solipsism we can’t apply experimental criticism since theories make equal predictions:
If the Inquisition’s theory were true, we should still expect the heliocentric theory to make accurate predictions of the results of all Earth-based astronomical observations, even though it would be factually false. It would therefore seem that any observations that appear to support the heliocentric theory lend equal support to the Inquisition’s theory. — page 77
As with solipsism we must apply the ‘hard to vary’ criterion. The assumption that planets move as if around the Sun, but they don’t and actually the Earth is at rest is — unexplained. More precisely, to understand Inquisitions theory we must first understand heliocentric theory, and then add an unnecessary assumption:
If the Inquisition had seriously tried to understand the world in terms of the theory they tried to force on Galileo, they would also have understood its fatal weakness, namely that it fails to solve the problem it purports to solve. It does not explain planetary motions ‘without having to introduce the complication of the heliocentric system’. On the contrary, it unavoidably incorporates that system as part of its own principle for explaining planetary motions. One cannot understand the world through the Inquisition’s theory unless one understands the heliocentric theory first.
Therefore we are right to regard the Inquisition’s theory as a convoluted elaboration of the heliocentric theory, rather than vice versa. We have arrived at this conclusion not by judging the Inquisition’s theory against modern cosmology, which would have been a circular argument, but by insisting on taking the Inquisition’s theory seriously, in its own terms, as an explanation of the world. — page 79
It is not that the heliocentric theory is right because it is simpler, or more intuitive. To claim that the Earth is moving is a counter-intuitive assumption. The difference is that Galileo explains why it feels like it’s at rest, and why it’s actually moving. On the other hand, Inquisition’s assumption is not explained, it is just postulated, and hence, easy to vary. We could say that the stars moves as if around the Sun, but actually its Jupiter that is at rest, not Earth.
4.5.0 How do we know whether something is real? What is the criteria for reality?
{4.4 On criterion changes. David defines the criteria in the Fabric of Reality which he improves upon in the Beginning of Infinity. I present his latest version. The old criterion is:
Dr Johnson’s criterion (My formulation) If it can kick back, it exists. A more elaborate version is: If, according to the simplest explanation, an entity is complex and autonomous, then that entity is real. — page 96 }
Something is real or exist as long as it appears in our best explanations of reality. This criterion applies to the example that David gives:
If you feel a sudden pain in your shoulder as you walk down a busy street, and look around, and see nothing to explain it, you may wonder whether the pain was caused by an unconscious part of your own mind, or by your body, or by something outside. You may consider it possible that a hidden prankster has shot you with an air-gun, yet come to no conclusion as to the reality of such a person. But if you then saw an air-gun pellet rolling away on the pavement, you might conclude that no explanation solved the problem as well as the air-gun explanation, in which case you would adopt it. In other words, you would tentatively infer the existence of a person you had not seen, and might never see, just because of that person’s role in the best explanation available to you. Clearly the theory of such a person’s existence is not a logical consequence of the observed evidence (which, incidentally, would consist of a single observation). Nor does that theory have the form of an ‘inductive generalization’, for example that you will observe the same thing again if you perform the same experiment. Nor is the theory experimentally testable: experiment could never prove the absence of a hidden prankster. Despite all that, the argument in favour of the theory could be overwhelmingly convincing, if it were the best explanation. — page 90
🧠 5 — Virtual Reality
David explains that human brain is like a virtual reality machine because we can render environments, both real and imaginary. Our perception of the world is a virtual reality created by our brain from its sensory inputs. Understanding involves comparing our reality with the external one; through scientific method we can improve our accuracy. This analogy makes it obvious that our reality is always fallible and inaccurate, for we don’t receive it from some ‘ultimate source’ — it is just our senses and guesses.
The main question of the chapter is:
What, if any, are its [virtual reality] ultimate limits? What sorts of environment can in principle be artificially rendered, and with what accuracy? By ‘in principle’ I mean ignoring transient limitations of technology, but taking into account all limitations that may be imposed by the principles of logic and physics. — page 103
Summary
Virtual reality machines can render logically possible, external experiences. They can’t factorize a prime number, nor give you a feeling that they did (for it would be an internal experience). Interestingly, the accuracy of a rendering can be ‘perfectly’ accurate, since we just need to figure out how to stimulate people brain nerves. Thus, in principle virtual reality could simulate any experience and emotion a person could ever feel, as accurately as we experience the real world itself.
But, how could we know whether something is a virtual reality or not? Laws of epistemology are universal. So we can find out only by disproving a virtual reality, never proving it.
Science and virtual reality rendering is the same process! Both are interested in simulating the physical world as accurately as possible. Thus, science is about getting a more accurate rendering of physical reality in ones brain. Einstein had a more accurate rendering ones he discovered general relativity, before his brain was running on Newtonian physics program.
What do we mean by “it was running on the Newtonian physics program”? Our perception of reality is based solely on electrical currents in our brain, yet we never experience them. So, what do we experience? A rendering of the reality that is done by our brain based on those currents. When we read symbols that represent Newtonian physics, we are imagining what they mean, and we are updating our view of reality. From then on, we are executing Newtonian physics, its code are symbols.
You can practice chapter questions as flashcards here.
5.1.0 What are the limits of experiences that virtual reality machines can render?
It can render a class of logically possible, external experiences.
We can simulate internal experiences (through drugs for instance), but David considers this to be a different technology — not VR.
VR cannot simulate logically impossible things, we can give someone a believe that this is possible, but that would be an internal experience (i.e. outside of VR definition).
5.1.1 What is the virtual reality repertoire?
The repertoire of a virtual-reality generator is the set of environments that the generator can be programmed to give the user the experience of. — page 122
In principle it can include all logically possible, external experiences. Yet, there are serious limitations to the set of programs that any virtual reality machine can have. As we shall see in the next chapter, it cannot have all possible programs of them — this would be an infinite set. {5.1 For explanation refer to the 6.2.0 card}
5.2.0 “What constraints, if any, do the laws of physics impose on the repertoires of virtual-reality generators?“ — page 105 We will consider this question in full next chapter, but first, let’s answer the part about its accuracy: What constraints do laws of physics impose on the accuracy of the images that virtual reality can render? {5.2 Note: an image is defined as “anything that gives rise to sensations”, thus smell and sound would be part of a rendering.}
Let’s consider plane in the free fall: Can virtual reality simulators render it? This turns out to be a complex problem, for we would have to combat gravity.
However, if one directly simulates nerves in a brain then any sensation we’ll feel be indistinguishably accurate. If we understand the brain and how it gives rise to senses, then we can simulate all possible experiences and feelings a human can have. Hence, the laws of physics impose no limit on the range and accuracy of images that virtual reality can render, for we would have to ‘fool’ only our senses.
5.3.0 Afterwards, David considers virtual reality environments that are interactive: your choices influence ‘images’ that are shown to you. We have shown that the accuracy of rendered images can be simulated as accurately as we could feel them. Yet: Can we ever 100% prove the accuracy of the rendered world?
Laws of epistemology are universal! They apply to the virtual universe just as much as to the physical one. In physical reality we can only disprove hypotheses, we can’t prove them (create positive evidence). Same goes for the virtual reality — we can only disprove the accuracy of the rendering environment, not prove it!
[the interactiveness of the virtual reality] gives rise to an important difference between image generation and virtual-reality generation. The accuracy of an image generator’s rendering can in principle be experienced, measured and certified by the user, but the accuracy of a virtual-reality rendering never can be. For example, if you are a music-lover and know a particular piece well enough, you can listen to a performance of it and confirm that it is a perfectly accurate rendering, in principle down to the last note, phrasing, dynamics and all. But if you are a tennis fan who knows Wimbledon’s Centre Court perfectly, you can never confirm that a purported rendering of it is accurate. Even if you are free to explore the rendered Centre Court for however long you like, and to ‘kick’ it in whatever way you like, and even if you have equal access to the real Centre Court for comparison, you cannot ever certify that the program does indeed render the real location. For you can never know what would have happened if only you had explored a little more, or looked over your shoulder at the right moment. Perhaps if you had sat on the rendered umpire’s chair and shouted ‘fault!’, a nuclear submarine would have surfaced through the grass and torpedoed the scoreboard. — page 115
5.4.0 What is the connection between science and virtual-reality generation?
Not only our virtual-reality renderings become more accurate as science progresses, but these processes, in a broad sense, are the same!
Consider this: as someone is reading the symbols that represent Newtonian physics, one imagines what they are like in ones brain. One internally renders a reality according to the Newtonian physics ‘program’.
Knowledge growth and virtual reality renderings are interlinked. When Einstein did a thought experiment of flying on a beam of light, he rendered a reality in his brain. It was a physically impossible one (for humans can’t flight on light beams), but it got him closer to rendering a reality that is more accurate than Newtonian physics — general relativity. When he imagined general relativity theory is his mind, he rendered the reality in his brain according to the general relativity ‘program’.
Thus science, in some sense, is about getting a virtual reality rendering in ones brain to accurately resemble external reality. In fact, how well the person understands reality depends on how well they can render it in ones brain.
5.3 How to build a better judgement?2
5.5.0 How brain is related to virtual reality?
Brain is the ‘ultimate’ virtual reality generator.
Imagination is a straightforward form of virtual reality. What may not be so obvious is that our ‘direct’ experience of the world through our senses is virtual reality too. For our external experience is never direct; nor do we even experience the signals in our nerves directly - we would not know what to make of the streams of electrical crackles that they carry. What we experience directly is a virtual-reality rendering, conveniently generated for us by our unconscious minds from sensory data plus complex inborn and acquired theories (i.e. programs) about how to interpret them.
We realists take the view that reality is out there: objective, physical and independent of what we believe about it. But we never experience that reality directly. Every last scrap of our external experience is of virtual reality. And every last scrap of our knowledge - including our knowledge of the non-physical worlds of logic, mathematics and philosophy, and of imagination, fiction, art and fantasy - is encoded in the form of programs for the rendering of those worlds on our brain’s own virtual-reality generator.
So it is not just science - reasoning about the physical world - that involves virtual reality. All reasoning, all thinking and all external experience are forms of virtual reality. — page 120
🧮 6 — Universality and the Limits of Computation
David explores what are the limits of virtual reality machines. He claims that it is possible to build a virtual-reality generator whose repertoire includes every physically possible environment. Hence, reality is comprehensible.
The heart of a virtual-reality generator is its computer, and the question of what environments can be rendered in virtual reality must eventually come down to the question of what computations can be performed. — page 123
The chapter’s main question is:
is there a single virtual-reality generator, buildable once and for all, that could be programmed to render any environment that the human mind is capable of experiencing? — page 123
Summary
To build a VR that simulates any physical environment we must start with the speed and memory constraints. David addresses speed by giving the machine ability to pause human mind until it computes the next step; by definition user would have no feeling of the pause. Memory is tackled by having a mechanism that adds and replaces memory disks.
Would this machine then have the repertoire of every physically possible environment? No. For they would have to be encoded in memory (for the program to run), and the best case scenario this is a numerable infinity. Yet, a set of every physically possible environment is not a numerable infinity. Latter is bigger than the former.
What is the difference? Can one infinity be bigger than the other? It can! We know it because of the Cantor’s argument. It says that a set of positive integers (0, 1, 2, 3 …) is smaller than all real numbers between 0 and 1. Difference is simple, you have a starting point 0 with positive integers, while you don’t with numbers between 0 and 1. Where do you start? At 0.00001? Or maybe 0.000000001? You can always add zero’s! Thus, when we compare infinities, by doing a one-to-one correspondence we can’t even start with the numbers between 0 and 1 set, so it is bigger.
But David doesn’t get upset, and rephrases the question to: Can we have a VR machine that has the repertoire of every other VR machine?
The answer is a resounding yes! Turing thought of a simple machine that only writes zeros and ones on a piece of paper. He then proved that it has the same repertoire as any other machine of that kind. This is called the Universal Turing Machine.
Computation is calculating an output from input by following a number of predefined rules. A mathematician is doing a computation. Hence, whatever he is doing can be done by the Universal Turing Machine. Universe can be seen as a computer calculating the output by following the laws of physics. Hence, Universal Turing Machine should be able to arbitrarily well simulate it. And if it is physically possible, it must have happened somewhere in the multiverse. Thus, laws of physics mandate their own comprehensibility.
You can practice chapter questions as flashcards here.
Cantor and Virtual Reality
6.1.0 How David addresses the speed and memory constraints of the virtual-reality machines?
In terms of memory, one can imagine a mechanism that provides supplementary disks of memory to the computer.
How would we deal with speed constraints? Some computations might take longer than required to give immediate response, and we can’t show ‘loading screen’ to the user! Once we design the computer increasing its speed would require changing its design, so we can’t apply the same trick as with memory.
David proposes a ‘technological’ trick. As discussed in the previous chapter, we would take control of the users brain, hence, we could ‘turn it off’ until our computation is finished. Turning it off means sending no signal, for user this wouldn’t feel like anything — pure absence of sensations. This means that 5 minutes in some virtual-reality environments would take 5 months of real time.
To achieve a perfect rendering of environments which call for a lot of computation, a virtual-reality generator would have to operate in something like the following way. Each sensory nerve is physically capable of relaying signals at a certain maximum rate, because a nerve cell which has fired cannot fire again until about one millisecond later. Therefore, immediately after a particular nerve has fired, the computer has at least one millisecond to decide whether, and when, that nerve should fire again. If it has computed that decision within, say, half a millisecond, no tampering with the brain’s speed is necessary, and the computer merely fires the nerve at the appropriate times. Otherwise, the computer causes the brain to slow down (or, if necessary, to stop) until the calculation of what should happen next is complete; it then restores the brain’s normal speed. — page 124
6.2.0: “By considering various tricks - nerve stimulation, stopping and starting the brain, and so on - we have managed to envisage a physically possible virtual-reality generator whose repertoire covers the entire sensory range, is fully interactive, and is not constrained by the speed or memory capacity of its computer. Is there anything outside the repertoire of such a virtual-reality generator? Would its repertoire be the set of all logically possible environments?” — page 126
As remarked in card 5.2.0 it won’t be, and it won’t be by a mile.
David uses Cantor’s diagonal argument to show that the repertoire of virtual-reality generator is not even close to the repertoire of all logically possible environments. The argument is about some infinities being bigger than others.
6.2.1 What is Cantor’s argument?
First, let’s clarify how do we know whether some infinities are as big as others. We start with trying to create an algorithm to enumerate each number in the infinite set. For positive integers we start with 0 and then add 1, so the algorithm is: n+1. For all positive even integers it would be: n+2, starting from 0. Using these algorithms, we do ‘one-to-one correspondence’ to prove that an infinite set of positive integers is just as big as an infinite set of even integers:
This is the defining characteristic of an infinite set — any part of it is as big as a whole.
Infinities are quite counter-intuitive, but it can get worst.
The essence of Cantor’s prove is that some infinities are enumerable (you have a starting point from which you can numerate them, like 0), while others aren’t. As we have shown, the infinity of positive integers is enumerable. Yet, the infinity of real numbers between 0 and 1 is non-enumerable — we start with … What? 0.00000001? Well no, because I could add another zero, and so on forever. Hence, there is no algorithm to list all the real numbers between 0 and 1 (Which has a very interesting implications in the theory of computation, but we’ll cover it in a bit!). This means that the infinite set of real numbers between 0 and 1 is bigger than the infinite set of positive integers. {If you are struggling to understand Cantor’s argument, this video might help.}
Coming back to our virtual-reality generator question. Whatever the repertoire of programs it has, they are listed in its memory. Even with infinite memory the matter of the fact is that they are listed. Yet, the set of all logically possible environments is unlistable (non-enumerable)! We can always find an environment that is not in the memory:
Now let us imagine this infinite set of possible programs arranged in an infinitely long list, and numbered Program 1, Program 2, and so on.
…
Let me define a class of logically possible environments which I shall call Cantgotu environments, partly in honour of Cantor, Godel and Turing, and partly for a reason I shall explain shortly. They are defined as follows. For the first subjective minute, a Cantgotu environment behaves differently from Environment 1 (generated by Program 1 of our generator). It does not matter how it does behave, so long as it is, to the user, recognizably different from Environment 1. During the second minute it behaves differently from Environment 2 (though it is now allowed to resemble Environment 1 again). During the third minute, it behaves differently from Environment 3, and so on. Any environment that satisfies these rules I shall call a Cantgotu environment.
…
Now, since a Cantgotu environment does not behave exactly like Environment 1, it cannot be Environment 1; since it does not behave exactly like Environment 2, it cannot be Environment 2. Since it is guaranteed sooner or later to behave differently from Environment 3, Environment 4 and every other environment on the list, it cannot be any of those either. But that list contains all the environments that are generated by every possible program for this machine. It follows that none of the Cantgotu environments are in the machine’s repertoire. The Cantgotu environments are environments that we can’t go to using this virtual-reality generator.
Clearly there are enormously many Cantgotu environments, because the definition leaves enormous freedom in choosing how they should behave, the only constraint being that during each minute they should not behave in one particular way. It can be proved that, for every environment in the repertoire of a given virtual-reality generator, there are infinitely many Cantgotu environments that it cannot render. — page 127, 128
Stronger Versions of the Turing Principle
6.3.0 One might get upset that our virtual-reality generator enterprise halted, but David perseveres with a new definition:
Since we cannot hope to render all logically possible environments, let us consider a weaker (but ultimately more interesting) sort of universality. Let us define a Universal virtual-reality generator as one whose repertoire contains that of every other physically possible virtual-reality generator. Can such a machine exist? — page 130
6.3.0 Answer
Virtual reality generator is just some form of computation. If there is a universal computer that can perform any computation that any other computer can, then it should be able to simulate any virtual reality generator. Thus, its repertoire would include the repertoire of any other virtual reality generator (Given enough time and memory!).
the feasibility of a universal virtual-reality generator depends on the existence of a universal computer - a single machine that can calculate anything that can be calculated. — page 131
6.3.1 Can such machine exist? What is the Church-Turing conjecture?
Yes, in principle, given enough time and memory, it can.
over a period of a few months in 1936, three mathematicians, Emil Post, Alonzo Church and, most importantly, Alan Turing, independently created the first abstract designs for universal computers. Each of them conjectured that his model of ‘computation’ did indeed correctly formalize the traditional, intuitive notion of mathematical ‘computation’. Consequently, each of them also conjectured that his model was equivalent to (had the same repertoire as) any other reasonable formalization of the same intuition. This is now known as the Church-Turing conjecture. — page 131
6.3.2 What is the Turing Machine?
Turing’s model of computation, and his conception of the nature of the problem he was solving, was the closest to being physical. His abstract computer, the Turing machine, was abstracted from the idea of a paper tape divided into squares, with one of a finite number of easily distinguishable symbols written on each square. Computation was performed by examining one square at a time, moving the tape backwards or forwards, and erasing or writing one of the symbols according to simple, unambiguous rules. Turing proved that one particular computer of this type, the universal Turing machine, had the combined repertoire of all other Turing machines. He conjectured that this repertoire consisted precisely of ‘every function that would naturally be regarded as computable’. He meant computable by mathematicians. — page 131
{6.2 On understanding Turing Machine. If you have hard time imagining it, watch this video. If you’d like to dive-in further into computation I highly recommend reading The Annotated Turing by Charles Petzold.}
6.4.0 Turing claimed that there is a universal computer that can calculate any function that any mathematician can compute. Can there be stronger versions of this principle?
mathematicians are rather untypical physical objects. Why should we assume that rendering them in the act of performing calculations is the ultimate in computational tasks? It turns out that it is not. As I shall explain in Chapter 9, quantum computers can perform computations of which no (human) mathematician will ever, even in principle, be capable. It is implicit in Turing’s work that he expected what ‘would naturally be regarded as computable’ to be also what could, at least in principle, be computed in nature. This expectation is tantamount to a stronger, physical version of the Church-Turing conjecture. The mathematician Roger Penrose has suggested that it should be called the Turing principle:
The Turing principle (for abstract computers simulating physical objects)
There exists an abstract universal computer whose repertoire includes any computation that any physically possible object can perform.
— page 132
6.4.1 How ‘Cantgotu’ environments relate to the Universal Turing Machine?
Computation is calculating an output from input by following a number of predefined rules. The fact that some infinities are non-enumerable means one cannot find some numbers by following a set of predefined rules. This means that some numbers are non-computable. Connecting the conclusions: the infinity of non-computable numbers is larger than the infinity of computable ones.
The proof I have given of the existence of Cantgotu environments is essentially due to Turing. As I said, he was not thinking explicitly in terms of virtual reality, but an ‘environment that can be rendered’ does correspond to a class of mathematical questions whose answers can be calculated. Those questions are computable. The remainder, the questions for which there is no way of calculating the answer, are called non-computable. — page 132
6.4.2 What connection of the Turing principle and virtual-reality generators one can make?
First, David establishes that any ‘genuine’ Universal Turing Machine must be physically realizable.
6.3 On this leap.
When I read this first time I didn’t buy it. Why ‘genuineness’ implies that computer is possible to build? How abstract became physical?
Yet, we should view this from the multiverse perspective (chapter 11 of The Beginning of Infinity). It claims that everything that is physically possible has happened somewhere in the multiverse (for it is infinite). Is Universal Turing Machine prohibited by the laws of physics? Its abstract notion implies that it isn’t. Hence, it is physically possible, and in fact, there is a universe in the multiverse that has made it.
the computing power of abstract machines has no bearing on what is computable in reality. The scope of virtual reality, and its wider implications for the comprehensibility of nature and other aspects of the fabric of reality, depends on whether the relevant computers are physically realizable. In particular, any genuine universal computer must itself be physically realizable. This leads to a stronger version of the Turing principle:
The Turing principle (for physical computers simulating each other)
It is possible to build a universal computer: a machine that can be programmed to perform any computation that any other physical object can perform.
— page 134
A virtual-reality generator is controlled by the Universal Turing Machine, and hence there is a virtual-reality generator that has a repertoire of every other virtual reality generator.
Summing up the Turing principle variations, one gets its strongest form:
The Turing principle
It is possible to build a virtual-reality generator whose repertoire includes every physically possible environment.
— page 135
6.4.3 What are the implications of the Turing principle in its strongest form?
The laws of physics mandate their own comprehensibility. If this machine is physically possible, someone in the multiverse has created it, thus someone has understood reality as accurately as one could. The laws of physics mandate a knower.
If the laws of physics as they apply to any physical object or process are to be comprehensible, they must be capable of being embodied in another physical object - the knower. It is also necessary that processes capable of creating such knowledge be physically possible. Such processes are called science. …
The laws of physics, by conforming to the Turing principle, make it physically possible for those same laws to become known to physical objects. Thus, the laws of physics may be said to mandate their own comprehensibility. …
Thus it follows from the Turing principle (in the strong form for which I have argued) that the laws of physics do not merely mandate their own comprehensibility in some abstract sense - comprehensibility by abstract scientists, as it were. They imply the physical existence, somewhere in the multiverse, of entities that understand them arbitrarily well. — page 135
6.5.0 If someone is contained within a virtual-reality with the wrong laws of physics can they ever understand something beyond it?
Yes! We are ‘constrained’ by the virtual reality in our brain and yet, we can understand phenomena beyond it.
Suppose that you are playing a virtual-reality video game. For the sake of simplicity, suppose that the game is essentially chess (a first-person-perspective version perhaps, in which you adopt the persona of the king). You will use the normal methods of science to discover this environment’s ‘laws of physics’ and their emergent consequences. You will learn that checkmate and stalemate are ‘physically’ possible events (i.e. possible under your best understanding of how the environment works), but that a position with nine white pawns is not ‘physically’ possible. Once you had understood the laws sufficiently well, you would notice that the chessboard is too simple an object to have, for instance, thoughts, and consequently that your own thought-processes can not be governed by the laws of chess alone. Similarly, you could tell that during any number of games of chess the pieces can never evolve into self-reproducing configurations. And if life cannot evolve on the chessboard, far less can intelligence evolve. Therefore you would also infer that your own thought-processes could not have originated in the universe in which you found yourself. — page 138
This argument depends on the believe that no clogged system can be self-sufficient in explanations. Good explanations can reach things that are unknown to their creator (like general relativity and quasars, see card 1.2.0), hence they could reach ‘beyond chess’.
The rendered environment would also have to be such that no explanations of anything inside would ever require one to postulate an outside. The environment, in other words, would have to be self-contained as regards explanations. But I doubt that any part of reality, short of the whole thing, has that property. — page 139
🗼 7 — A Conversation About Justification
David explains the modern problem of induction, and how this is not a problem at all. Inductivists search for the justification of the theory, but all our knowledge is just a guess, some better than others. There is no way to justify the guesses we make, only to refute them in search of the better ones.
{7.1 On David’s use of the justification word. In his commentary for the audiobook version of The Fabric of Reality David says that one of the things he regrets is the usage of the word justified throughout this chapter. He believes one can deal without it. Instead of treating the word as ‘proving’ something, regard it as: being in line with something.}
Summary
The modern problem of induction is that humans don’t understand how can we prefer one theory over the other if we don’t have a positive evidence for it. Since, I can create infinite number of theory’s variations, how would I choose between them? For example, I make up a Mark-float general relativity. Everything is just like in the general relativity, but when I jump from high places I would float instead.
Assume we follow Popper and test this theory experimentally, I jump from a high place, and unsurprisingly, ascend and die. Could we disprove such theories without experimental test? For if we can’t than I can make up 8-billion different versions of the general relativity (for each human on Earth). Why do we trust the original general relativity over its infinite counterparts?
The absence of a good explanation for this choice is the modern problem of induction (it has a few other traits, I leave them out for brevity). We have seen a similar problem before in the Criteria of Reality chapter. The answer is the same: We refute all those 8 billion theories for they add a needless assumption that is easy to vary. But general relativity in its original view does not.
You can practice chapter questions as flashcards here.
Induction and Justification
7.1.0 What is the modern problem of induction?
People understand that induction is wrong, but they don’t understand why any scientific theory should be a reliable basis for action if no logical reasoning can rule out one theory over the other. The absence of positive argument or evidence is a problem because we can’t justify preferring one theory over the other.
why should a better explanation be what we always assume it to be in practice, namely the token of a truer theory? Why, for that matter, should a downright bad explanation (one that has none of the above attributes, say) necessarily be false? There is indeed no logically necessary connection between truth and explanatory power. A bad explanation (such as solipsism) may be true. Even the best and truest available theory may make a false prediction in particular cases, and those might be the very cases in which we rely on the theory. No valid form of reasoning can logically rule out such possibilities, or even prove them unlikely. But in that case, what justifies our relying on our best explanations as guides to practical decision-making? More generally, whatever criteria we used to judge scientific theories, how could the fact that a theory satisfied those criteria today possibly imply anything about what will happen if we rely on the theory tomorrow? …
I wish to redefine the term ‘inductivist’ to mean someone who believes that the invalidity of inductive justification is a problem for the foundations of science. In other words, an inductivist believes that there is a gap which must be filled, if not by a principle of induction then by something else. — page 143
7.2.0 What is a justification?
Justification implies proving something right, same as creating a positive argument or evidence. To justify a theory would mean to prove that it is a 100% truth.
Debunking Crypto-Inductivists
7.3.0 What are the four main believes that crypto-inductivists hold that David would challenge? {7.2 Crypto-inductivist is a person who believes that the problem of induction exists and it is a gap in science that must be filled.}
They desire a 100% certainty to make decisions.
There must be some way to justify (create positive evidence for) theories because this is the only way to differentiate between the infinite set of theory’s potential rivals (variations).
They believe that the future resembles the past in some manner.
They believe that our knowledge must be based on some justified, secure foundations to be reliable.
7.4.0 What is the refutation of the first main believe that crypto-inductivists hold? {7.3 Belief: They desire a 100% certainty to make decisions.}
This goes against the nature of the tools we have. We use language, senses and brain, all of which are profoundly error-prone. Hence, they fail to understand that we are unlikely to ever reach 100% truth.
Also, since knowledge creation is about refutation, how exactly are we suppose to reach 100% certain truth?
7.5.0 Elaborate on the second main believe that crypto-inductivists hold. What are their arguments? {7.4 Belief: There must be some way to justify (create positive evidence for) theories because this is the only way to differentiate between the infinite set of theory’s potential rivals (variations).}
There must be some way to justify (create positive evidence for) theories. Otherwise, we can’t differentiate between an infinite set of its potential variations. Popperian epistemology tells us what not to believe in, not what to believe. It can only refute theories once they are presented, but this negates the question of: Why should we choose one theory’s version over its rivals? Because all the others were refuted? But we can create 100s of rivals in a minute, in fact, there is an infinite set of those rivals. Thus, we can’t rely only on falsification, we need something that helps to find the needle in the hay, and that is a positive evidence for a theory. And its absence is the problem of induction.
Here is the example for general relativity that we were referring to in regards to creating 100s of rivals:
‘Whenever you, David, jump from high places in ways that would, according to the prevailing theory, kill you, you float instead. Apart from that, the prevailing theory holds universally.’ I put it to you that every past test of your theory was also necessarily a test of mine, since all the predictions of your theory and mine regarding past experiments are identical. Therefore your theory’s refuted rivals were also my theory’s refuted rivals. And therefore my new theory is exactly as corroborated as your prevailing theory. How, then, can my theory be ‘untenable’? What faults could it possibly have that are not shared by your theory? — page 151
And obviously if you falsify the ‘David-float’ variation of general relativity, we could create ‘Mark-float’ variation and so on, we can have at least 7 billion of those variations (and then proceed from humans to objects). Why should I believe one over another?
7.5.1 What is its criticism?
This is an epistemological breakthrough that David discovered in his last book — The Beginning of Infinity. You differentiate between those theories by imposing a ‘hard to vary’ criterion. The person that has ‘float powers’ is easily varied, there is no inherent explanation of why it should be David over someone else. Because general relativity has no parts that could be easily changed without collapsing the entire theory, it is preferred as an explanation of the world over rivals. If someone presents not a variation of general relativity, but genuinely new theory that is also hard to vary, we would have to perform crucial experimental test to adjudicate.
7.5 On crucial experimental test.
In the ‘easily varied’ examples of general relativity that crypto-inductivists bring we don’t have to experimentally test it because we can refute those theories with the philosophical argument (see cards 1.7.0 and 4.3.0). But imagine we have to falsify them experimentally: How would a crucial experimental test look like?
Answer.
Let’s consider general relativity vs its David-float variation. We have to find an experiment where theories would diverge in predictions. By theory’s name we can tell it is in David’s ability to float. So the crucial experimental test would involve throwing David off a high-ground and observing whether he floats.
To remind yourself of the crucial experimental test see card 3.4.0.
7.6.0 Elaborate on the third main believe that crypto-inductivists hold. What are their arguments? {7.6 Belief: The future resembles the past in some manner.}
Even if your ‘hard to vary’ criterion refutes our second believe, it justifies our third one! For hard to vary criterion justified choosing one theory over another, hence the theory applies both to present and future, they must resemble each other in some manner.
you have justified a theory about the future (the prevailing theory of gravity) as being more reliable than another theory (the one I proposed), even though they are both consistent with all currently known observations. Since the prevailing theory applies both to the future and to the past, you have justified the proposition that, as regards gravity, the future resembles the past. And the same would hold whenever you justify a theory as reliable on the grounds that it is corroborated. Now, in order to go from ‘corroborated’ to ‘reliable’, you examined the theories’ explanatory power. So what you have shown is that what we might call the ‘principle of seeking better explanations’, together with some observations - yes, and arguments - imply that the future will, in many respects, resemble the past. — page 157
7.6.1 What is its criticism?
This idea implies that we could derive some knowledge about the future from the past, but this is not the process that we are following. It is not that ‘David-float’ anomaly has not happened in the past, so it won’t happen in the future, it is that we don’t have good explanation behind it. With the good explanation, even if some anomaly has never happened before, we conclude reliably that it will happen.
DAVID: You say this implies that ‘the future resembles the past’. Well, vacuously, yes, inasmuch as any theory about the future would assert that it resembled the past in some sense. But this inference that the future resembles the past is not the sought-for principle of induction, for we could neither derive nor justify any theory or prediction about the future from it. For example, we could not use it to distinguish your theory of gravity from the prevailing one, for they both say, in their own way, that the future resembles the past.
CRYPTO-INDUCTIVIST: Couldn’t we derive, from the ‘explanation principle’, a form of the principle of induction that could be used to select theories? What about: ‘if an unexplained anomaly does not happen in the past, then it is unlikely in the future’?
DAVID: No. Our justification does not depend on whether a particular anomaly happens in the past. It has to do with whether there is an explanation for the existence of that anomaly. — page 158
7.7.0 Elaborate on the fourth main believe that crypto-inductivists hold. What are their arguments? {7.7 Belief: Our knowledge must be based on some justified, secure foundations to be reliable.}
Be it truths of pure logic or some other foundation of our knowledge, we must build it on something secure and justified.
We have seen that future predictions can be justified by appeal to the principles of rationality. [they refer to the ‘hard to vary’ criterion] But what justifies those? They are not, after all, truths of pure logic. So there are two possibilities: either they are unjustified, in which case conclusions drawn from them are unjustified too; or they are justified by some as yet unknown means. In either case there is a missing justification. — page 163
7.7.1 What is its criticism?
There is no secure foundation of truth, be it logic or math. All our knowledge comes from fallible, error-prone tools. We might like to have some security, but we can never escape the fact that we access the world through imperfect tools and senses, which are inherently fallible. This implies that our knowledge of any subject (from psychology to physics and math) can be wrong. **To hope or search for justification without addressing this issue (i.e. fallibility of our tools and senses) first is to misunderstand the root of the fallibility problem.
It is not perfectly secure. Nor should we expect it to be, for logical reasoning is no less a physical process than scientific reasoning is, and it is inherently fallible. The laws of logic are not self-evident. There are people, the mathematical ‘intuitionists’, who disagree with the conventional laws of deduction (the logical ‘rules of inference’). I discuss their strange world-view in Chapter 10 of The Fabric of Reality. They cannot be proved wrong, but I shall argue that they are wrong, and I am sure you will agree that my argument justifies this conclusion. — page 163
🌱 8 — The Significance of Life
How do we know whether something is alive or not? On first glance the answer seems to be in genes (the replicating molecules). But when questioned closer we understand that the true universal premise is about knowledge.
What are the implication on the universe of this idea? All in this chapter.
Summary
Molecules are basis of life. A replicator is something that causes an environment to replicate itself, because it can’t do it on its own, like a song or a molecule.
Replicator molecules are called genes. Gene’s environment is called a niche. Some niches are more suitable to genes than others. The more gene replicates in a niche, the better it represents some fundamental knowledge about the niche. Song can only be replicated by people, the more viral song is, the better it embodies some profound knowledge about the people that listen to it (i.e. replicate).
A popular misconception is that all organisms are replicators, David says this is false, molecules are the one that get actually replicated. (I challenge this idea.)
Virtual reality is related to evolution for they are doing the same function — both are trying to embody some profound truth about the environment they are in. If they do the job poorly, they are discarded. Virtual reality is trying to be as accurate simulation of the real world as possible, while genes are trying to replicate as much as possible.
However, replication can not be the essence of life. For I can imagine a species that doesn’t replicate, but tries to preserve itself by constant maintenance. The better it is at adapting to the environment, the more it will survive. (I challenge this idea as there would be an evolution of adaptation/ ideas within that being.)
So what is the basis of life? It is in the embodiment of knowledge about the entities niche. Moreover, as life seems to be the only thing that creates knowledge, it is the means through which the strongest version of the Turing Principle becomes reality (that it is possible to build a machine that arbitrarily well simulates reality itself).
Humans and life are significant for they are the only ones that create knowledge. Knowledge has an immense bearing on what the universe will be in the long-run. Just as it had impact on how the landscape of our planet looks like. Thus, humans are cosmically significant.
You can practice chapter questions as flashcards here.
DNA, Genes and Replicators
8.1.0 What is the basis of life?
The basis of life is molecular.
Modern biology does not try to define life by some characteristic physical attribute or substance - some living ‘essence’ - with which only animate matter is endowed. We no longer expect there to be any such essence, because we now know that ‘animate matter’, matter in the form of living organisms, is not the basis of life. It is merely one of the effects of life, and the basis of life is molecular. It is the fact that there exist molecules which cause certain environments to make copies of those molecules. — page 170
8.2.0 What is a replicator?
In a broad sense it is something that causes the environment to replicate itself — like a song, or a molecule.
Such molecules are called replicators. More generally, a replicator is any entity that causes certain environments to copy it. Not all replicators are biological, and not all replicators are molecules. For example, a self-copying computer program (such as a computer virus) is a replicator. A good joke is another replicator, for it causes its listeners to retell it to further listeners. Richard Dawkins has coined the term meme (rhyming with ‘cream’) for replicators that are human ideas, such as jokes. — page 170
8.2.1 Is anything that can be copied a replicator?
No. The replicator can’t replicate itself without the environment. A song can be spread only by its listeners (i.e. environment). The replicator causes its replication, if it is replaced by a random object an environment won’t spread it (depending on the song people will share it or not, not any song goes).
Not everything that can be copied is a replicator. A replicator causes its environment to copy it: that is, it contributes causally to its own copying. … What it means in general to contribute causally to some thing is an issue to which I shall return, but what I mean here is that the presence and specific physical form of the replicator makes a difference to whether copying takes place or not. In other words, the replicator is copied if it is present, but if it were replaced by almost any other object, even a rather similar one, that object would not be copied. … The presence of the gene in its proper form and location makes a difference to whether copying takes place, which makes it a replicator, though there are countless other causes contributing to its replication as well. — page 172
8.3.0 What are genes and DNA?
Molecules that cause the environment to replicate themselves are called genes.
But all life on Earth is based on replicators that are molecules. These are called genes, and biology is the study of the origin, structure and operation of genes, and of their effects on other matter. In most organisms a gene consists of a sequence of smaller molecules, of which there are four different kinds, joined together in a chain. The names of the component molecules (adenine, cytosine, guanine and thymine) are usually shortened to A, C, G and T. The abbreviated chemical name for a chain of any number of A, C, G and T molecules, in any order, is DNA. — page 171
8.3.1 What is the essence of genes? What do they do?
They can be seen as computer program for living beings.
Genes are in effect computer programs, expressed as sequences of A, C, G and T symbols in a standard language called the genetic code which, with very slight variations, is common to all life on Earth. (Some viruses are based on a related type of molecule, RNA, while prions are, in a sense, self-replicating protein molecules.) Special structures within each organism’s cells act as computers to execute these gene programs. The execution consists of manufacturing certain molecules (proteins) from simpler molecules (amino acids) under certain external conditions. For example, the sequence ‘ATG ‘ is an instruction to incorporate the amino acid methionine into the protein molecule being manufactured. — page 171
8.3.2 How do they work?
Typically, a gene is chemically ‘switched on’ in certain cells of the body, and then instructs those cells to manufacture the corresponding protein. For example, the hormone insulin, which controls blood sugar levels in vertebrates, is such a protein. The gene for manufacturing it is present in almost every cell of the body, but it is switched on only in certain specialized cells in the pancreas, and then only when it is needed. At the molecular level, this is all that any gene can program its cellular computer to do: manufacture a certain chemical. But genes succeed in being replicators because these low-level chemical programs add up, through layer upon layer of complex control and feedback, to sophisticated high-level instructions. Jointly, the insulin gene and the genes involved in switching it on and off amount to a complete program for the regulation of sugar in the bloodstream.
Similarly, there are genes which contain specific instructions for how and when they and other genes are to be copied, and instructions for the manufacture of further organisms of the same species, including the molecular computers which will execute all these instructions again in the next generation. There are also instructions for how the organism as a whole should respond to stimuli - for instance, when and how it should hunt, eat, mate, fight or run away. And so on. — page 171
8.3.3 How does environment affect the genes replicator function?
Genes replicator function entirely depends on its environment: its niche; just as any other living organism.
A gene can function as a replicator only in certain environments. By analogy with an ecological ‘niche’ (the set of environments in which an organism can survive and reproduce), I shall also use the term niche for the set of all possible environments which a given replicator would cause to make copies of it. The niche of an insulin gene includes environments where the gene is located in the nucleus of a cell in the company of certain other genes, and the cell itself is appropriately located within a functioning organism, in a habitat suitable for sustaining the organism’s life and reproduction. But there are also other environments - such as biotechnology laboratories in which bacteria are genetically altered so as to incorporate the gene - which likewise copy the insulin gene. Those environments are also part of the gene’s niche, as are an infinity of other possible environments that are very different from those in which the gene evolved. — page 172
8.3.4 What is the degree of adaptation? How do we identify its extent?
The degree to which a replicator contributes causally to its own replication. The more inflexible the replicator is to still be replicated, the higher degree of adaptation it has. For example junk DNA sequences have low degree of adaptation because they could be highly varied and still copied.
the degree of adaptation of a replicator to a given environment as the degree to which the replicator contributes causally to its own replication in that environment. If a replicator is well adapted to most environments of a niche, we may call it well adapted to the niche. We have just seen that the insulin gene is highly adapted to its niche. Junk DNA sequences have a negligible degree of adaptation by comparison with the insulin gene, or any other bona fide gene, but they are far more adapted to that niche than most molecules are. — page 173
8.1 My thoughts on adaptation.3
8.4.0 What are junk DNA sequences?
Along with genes, random sequences of A, C, G and T, sometimes called junk DNA sequences, are present in the DNA of most organisms. They are also copied and passed on to the organisms’ offspring. However, if such a sequence is replaced by almost any other sequence of similar length, it is still copied. So we can infer that the copying of such sequences does not depend on their specific physical form. Unlike genes, junk DNA sequences are not programs. If they have a function (and it is not known whether they do), it cannot be to carry information of any kind. — page 173
{8.2 On junk DNA function: It is now known that ‘junk’ DNA has a regulatory function of gene expression (and many others), so scientists refer to it as non-coding DNA. In fact, humans consist of 98-99% of non-coding DNA!}
8.5.0 What is usually the most important factor determining the gene’s niche?
The presence of other genes it needs for replication!
The most important factor determining a gene’s niche is usually that the gene’s replication depends on the presence of other genes. For example, the replication of a bear’s insulin gene depends not only on the presence, in the bear’s body, of all its other genes, but also on the presence, in the external environment, of genes from other organisms. Bears cannot survive without food, and the genes for manufacturing that food exist only in other organisms. — page 175
8.6.0 What is the misconception that people have about organisms?
An organism is not a replicator: it is part of the environment of replicators - usually the most important part after the other genes. The remainder of the environment is the type of habitat that can be occupied by the organism (such as mountain tops or ocean bottoms) and the particular lifestyle within that habitat (such as hunter or filter-feeder) which enables the organism to survive for long enough for its genes to be replicated.
…
we think of organisms as replicators. But this is inaccurate. Organisms are not copied during reproduction; far less do they cause their own copying. They are constructed afresh according to blueprints embodied in the parent organisms’ DNA. For example, if the shape of a bear’s nose is altered in an accident, it may change the lifestyle of that particular bear, and the bear’s chances of surviving to ‘reproduce itself ‘ may be affected for better or worse. But the bear with the new shape of nose has no chance of being copied. If it does have offspring, they will have noses of the original shape. But make a change in the corresponding gene (if you do it just after the bear is conceived, you need only change one molecule), and any offspring will not only have noses of the new shape, but copies of the new gene as well. This shows that the shape of each nose is caused by that gene, and not by the shape of any previous nose. So the shape of the bear’s nose makes no causal contribution to the shape of the offspring’s nose. But the shape of the bear’s genes contributes both to their own copying and to the shape of the bear’s nose and of its offspring’s nose. So an organism is the immediate environment which copies the real replicators: the organism’s genes. — page 175
8.2 My thoughts on an organism as a replicator.4
Turing Principle and Evolution
8.7.0 How is virtual reality related to evolution and organisms? Explain the analogy.
External habitat is the user for whom the rendering is created.
The organism created is the rendered virtual-reality.
The adaptations of the genes to the niche is the level of accuracy of the rendered virtual-reality.
If the external habitat (user) perceives the organism (rendered virtual-reality) to have low adaptation (inaccurate rendering) then it doesn’t replicate (survive).
As I have said, all virtual-reality rendering physically manufactures the rendered environment. The inside of any virtual-reality generator in the act of rendering is precisely a real, physical environment, manufactured to have the properties specified in the program. It is just that we users sometimes choose to interpret it as a different environment, which happens to feel the same. As for the absence of a user, let us consider explicitly what the role of the user of virtual reality is. First, it is to kick the rendered environment and to be kicked back in return - in other words, to interact with the environment in an autonomous way. In the biological case, that role is performed by the external habitat. Second, it is to provide the intention behind the rendering. That is to say, it makes little sense to speak of a particular situation as being a virtual-reality rendering if there is no concept of the rendering being accurate or inaccurate. I have said that the accuracy of a rendering is the closeness, as perceived by the user, of the rendered environment to the intended one. But what does accuracy mean for a rendering which no one intended and no one perceives? It means the degree of adaptation of the genes to their niche. We can infer the ‘intention’ of genes to render an environment that will replicate them, from Darwin’s theory of evolution. Genes become extinct if they do not enact that ‘intention’ as efficiently or resolutely as other competing genes. — page 178
8.7.1 What are the implications of this analogy?
That genes, just as virtual-reality renderings, embody knowledge about the reality.
So living processes and virtual-reality renderings are, superficial differences aside, the same sort of process. Both involve the physical embodying of general theories about an environment. In both cases these theories are used to realize that environment and to control, interactively, not just its instantaneous appearance but also its detailed response to general stimuli.
Genes embody knowledge about their niches. — page 179
8.7.2 Can one remove the idea of replicators from this reasoning?
Yes.
Everything of fundamental significance about the phenomenon of life depends on this property, and not on replication per se. So we can now take the discussion beyond replicators. In principle, one could imagine a species whose genes were unable to replicate, but instead were adapted to keep their physical form unchanged by continual self maintenance and by protecting themselves from external influences. Such a species is unlikely to evolve naturally, but it might be constructed artificially. Just as the degree of adaptation of a replicator is defined as the degree to which it contributes causally to its own replication, we can define the degree of adaptation of these non-replicating genes as the degree to which they contribute to their own survival in a particular form. — page 179
8.7.3 What then, is the essence of life?
It is not in the molecules replication, but in the embodiment of the knowledge about the niches.
It is the survival of knowledge, and not necessarily of the gene or any other physical object, that is the common factor between replicating and non-replicating genes. … The point is that although all known life is based on replicators, what the phenomenon of life is really about is knowledge. We can give a definition of adaptation directly in terms of knowledge: an entity is adapted to its niche if it embodies knowledge that causes the niche to keep that knowledge in existence. — page 181
8.8.0 How can we connect the Turing principle in its strongest form (there must be a knower who understood reality sufficiently well) with the essence of life as we have defined it?5
Life is the means through which the Turing principle gets realized.
Life is about the physical embodiment of knowledge, and in Chapter 6 we came across a law of physics, the Turing principle, which is also about the physical embodiment of knowledge. It says that it is possible to embody the laws of physics , as they apply to every physically possible environment, in programs for a virtual-reality generator. Genes are such programs. Not only that, but all other virtual-reality programs that physically exist, or will ever exist, are direct or indirect effects of life. For example, the virtual-reality programs that run on our computers and in our brains are indirect effects of human life. So life is the means - presumably a necessary means - by which the effects referred to in the Turing principle have been implemented in nature. — page 181
8.8.1 What is the counterargument for this reasoning?
It is an anthropocentric, parochial reasoning that has no effect on the universe as a whole. We value knowledge only because it is fundamental to our survival. It has no meaningful bearing on the universe.
I have not yet established that the Turing principle itself has the status of a fundamental law. A sceptic might argue that it does not. It is a law about the physical embodiment of knowledge, and the sceptic might take the view that knowledge is a parochial, anthropocentric concept rather than a fundamental one. That is, it is one of those things which is significant to us because of what we are - animals whose ecological niche depends on creating and applying knowledge - but not significant in an absolute sense. To a koala bear, whose ecological niche depends on eucalyptus leaves, eucalyptus is significant; to the knowledge-wielding ape Homo sapiens, knowledge is significant. — page 182
8.8.2 Does knowledge have a significant bearing on the universe?
It does, and even though large physical impact is not the decisive criterion, it certainly is relevant. Let’s break down its impact on astrophysics:
We can use the [stellar evolution theory] to predict the future development of the Sun. It says that the Sun will continue to shine with great stability for another five billion years or so; then it will expand to about a hundred times its present diameter to become a red giant star; then it will pulsate, flare into a nova, collapse and cool, eventually becoming a black dwarf. But will all this really happen to the Sun? Has every star that formed a few billion years before the Sun, with the same mass and composition, already become a red giant, as the theory predicts? Or is it possible that some apparently insignificant chemical processes on minor planets orbiting those stars might alter the course of nuclear and gravitational processes having overwhelmingly more mass and energy?
If the Sun does become a red giant, it will engulf and destroy the Earth. If any of our descendants, physical or intellectual, are still on the Earth at that time, they might not want that to happen. They might do everything in their power to prevent it.
Is it obvious that they will not be able to? Certainly, our present technology is far too puny to do the job. But neither our theory of stellar evolution nor any other physics we know gives any reason to believe that the task is impossible. On the contrary, we already know, in broad terms, what it would involve (namely, removing matter from the Sun). And we have several billion years to perfect our half-baked plans and put them into practice. If, in the event, our descendants do succeed in saving themselves in this way, then our present theory of stellar evolution, when applied to one particular star, the Sun, gives entirely the wrong answer. And the reason why it gives the wrong answer is that it does not take into account the effect of life on stellar evolution. It takes into account such fundamental physical effects as nuclear and electromagnetic forces, gravity, hydrostatic pressure and radiation pressure - but not life. — page 183
Significance of Life
8.9.0 Why life is significant?
Besides it being the means of realizing the Turing principle, it will decide the fate of universe (or big part of it). If one wants to predict and understand the universe, one would have to understand life, its culture, morality and technology, for its decisions will be the shape such of massive astrophysical objects as stars, planets and galaxies.
the point I am making here does not depend on our being able to predict what will happen, but only on the proposition that what will happen will depend on what knowledge our descendants have, and on how they choose to apply it. Thus one cannot predict the future of the Sun without taking a position on the future of life on Earth, and in particular on the future of knowledge. The colour of the Sun ten billion years hence depends on gravity and radiation pressure, on convection and nucleosynthesis. It does not depend at all on the geology of Venus, the chemistry of Jupiter, or the pattern of craters on the Moon. But it does depend on what happens to intelligent life on the planet Earth. It depends on politics and economics and the outcomes of wars. It depends on what people do: what decisions they make, what problems they solve, what values they adopt, and on how they behave towards their children. …
even if the human race will in the event fail in its efforts to survive, does the pessimistic theory apply to every extraterrestrial intelligence in the universe? If not - if some intelligent life, in some galaxy, will ever succeed in surviving for billions of years - then life is significant in the gross physical development of the universe. — page 184
8.10.0 Are there any immediate physical attributes that differentiate knowledge-bearing and non-knowledge bearing objects (not their remote effects in the future)?
Remarkably, there is. To see what it is, we must take the multiverse view. — page 187
8.10.1 Imagine a bear’s genome, some parts of it contain genes, some junk DNA. The genes contain useful information (the embodied knowledge of its niche), and junk DNA doesn’t.
Consider a DNA sequence that is: TCGTCGTTTC. Imagine that this exact sequence is both present in the genes and the junk DNA. They are exactly physically alike, yet one contains knowledge and the other one doesn’t. How could we distinguish between them?
How can knowledge be a fundamental physical quantity, if one object has it while a physically identical object does not? — page 188
Answer.
From the subjective, single-universe perspective they might seem identical, but let’s imagine the multiverse perspective. The useful information in the gene embodies some knowledge about the niche bears live in, this would cause gene TCGTCGTTTC sequence to replicate and survive over time. The junk DNA TCGTCGTTTC sequence has no embodied knowledge, so it doesn’t contribute to its replication. Hence, it isn’t resilient across time and universes (it is easily varied). If one takes the god-eye-view on the multiverse, one would see that in the universes where bears exists the gene TCGTCGTTTC segment is spread across them, while non-gene segment isn’t.
the bear’s gene segment must have the same sequence in almost all nearby universes as it does in ours. That is because it is presumably highly adapted, which means that most variants of it would not succeed in getting themselves copied in most variants of their environment, and so could not appear at that location in the DNA of a living bear. In contrast, when the non-knowledge-bearing DNA segment undergoes almost any mutation, the mutated version is still capable of being copied. Over generations of replication many mutations will have occurred, and most of them will have had no effect on replication. Therefore the junk-DNA segment, unlike its counterpart in the gene, will be thoroughly heterogeneous in different universes. It may well be that every possible variation of its sequence is equally represented in the multiverse (that is what we should mean by its sequence being strictly random).
So the multiverse perspective reveals additional physical structure in the bear’s DNA. In this universe, it contains two segments with the sequence TCGTCGTTTC. One of them is part of a gene, while the other is not part of any gene. In most other nearby universes, the first of the two segments has the same sequence, TCGTCGTTTC, as it does in our universe, but the second segment varies greatly between nearby universes. So from the multiverse perspective the two segments are not even remotely alike (Figure 8.1). — page 189
8.10.2 What are the implications of this idea?
8.3 On objective morality and aesthetics in the multiverse.
How to physically differentiate between better and worse moral and aesthetic theories?6
It’s not that life is physically special, but knowledge-bearing entities are, and life is the only thing known to us that creates knowledge.
Again we were too parochial, and were led to the false conclusion that knowledge-bearing entities can be physically identical to non knowledge-bearing ones; and this in turn cast doubt on the fundamental status of knowledge. But now we have come almost full circle. We can see that the ancient idea that living matter has special physical properties was almost true: it is not living matter but knowledge-bearing matter that is physically special. Within one universe it looks irregular; across universes it has a regular structure, like a crystal in the multiverse. — page 190
If one perceives from the subjective, single-universe perspective it might seem that galaxies are the most significant creations. Yet, if one takes the multiverse perspective, then embodied knowledge is the largest distinctive structure, and those that create it — life. {8.5 On knowledge forms: This idea is closely related with the fundamental notion in the Beginning of Infinity that: Knowledge is substrate independent.}
Finally, let us look around the universe in a similar way. What will catch our magically enhanced eye? In a single universe the most striking structures are galaxies and clusters of galaxies. But those objects have no discernible structure across the multiverse. Where there is a galaxy in one universe, a myriad galaxies with quite different geographies are stacked in the multiverse. And so it is everywhere in the multiverse. Nearby universes are alike only in certain gross features, as required by the laws of physics, which apply to them all. Thus most stars are quite accurately spherical everywhere in the multiverse, and most galaxies are spiral or elliptical. But nothing extends far into other universes without its detailed structure changing unrecognizably. Except, that is, in those few places where there is embodied knowledge. In such places, objects extend recognizably across large numbers of universes. Perhaps the Earth is the only such place in our universe, at present. In any case, such places stand out, in the sense I have described, as the location of the processes - life, and thought - that have generated the largest distinctive structures in the multiverse. — page 192
🪮 9 — Quantum Computers
The questions that we answer in this chapter:
What are quantum computers?
What tasks they can do better than classical ones?
How is chaos theory disproved by quantum physics?
Why quantum physics is random for us, but deterministic objectively?
Summary
A quantum computer is a computer that uses other universes to perform parts of its computation. It then assembles their results with its own and gives the final answer. This makes it significantly faster than any classical computer.
Computation complexity theory studies how efficiently in principle a task can be done. A task is computationally intractable if time to perform it increases exponentially. Many intractable tasks for classical computers are more than tractable for the quantum ones.
Chaos theory says that a butterfly can cause a hurricane, but this is only in classical physics. It says so because in classical physics things are unpredictable because they can never measure things accurately enough (for everything is continuous, so you can always improve accuracy). And as you simulate the model small deviations in measurements produce wildly different results.
But reality is quantum, and matter is discrete. So we can measure things sufficiently accurately. Butterflies don’t cause hurricanes. What happens is that we subjectively perceive hurricane or not, but in the multiverse both scenarios have played out. Since butterflies are so small and inconsequential, they don’t impact the measure across the multiverse of hurricanes happening (say it’s 50/50, and with butterfly it stays around the same 50/50).
Thus, this is why quantum physics is subjectively random for us (as we observe only one scenario happening), while objectively it is deterministic (as all scenario will play out).
Shor’s algorithm is a program that can be run on quantum computers to do factorization of a very large numbers. It is intractable for classical one and all our modern security is based on it. If there are no parallel universes, and multiverse is wrong: Where Shor’s algorithm is performing computation? The atoms in our visible universe wouldn’t be enough for it. Where does it take the resources to compute things on? The answer was long obvious to those that seek explanations of the world — parallel universes.
You can practice chapter questions as flashcards here.
Quantum Computers and Computation Complexity Theory
9.1.0 What is a quantum computer? What makes it a distinctly different paradigm of computation?
Classical computers calculate things using our universe. Quantum computers use multiple universes at once to calculate different parts of the task and then share the results.
Quantum computation is more than just a faster, more miniaturized technology for implementing Turing machines. A quantum computer is a machine that uses uniquely quantum-mechanical effects, especially interference, to perform wholly new types of computation that would be impossible, even in principle, on any Turing machine and hence on any classical computer. Quantum computation is therefore nothing less than a distinctively new way of harnessing nature. …
There followed thousands of years of progress in this type of technology - harnessing some of the materials, forces and energies of physics. In the twentieth century information was added to this list when the invention of computers allowed complex information processing to be performed outside human brains. Quantum computation, which is now in its early infancy, is a distinct further step in this progression. It will be the first technology that allows useful tasks to be performed in collaboration between parallel universes. A quantum computer would be capable of distributing components of a complex task among vast numbers of parallel universes, and then sharing the results. — page 195
9.2.0 Many people criticize the universality of computation (and virtual-reality rendering) for its impracticality. It is a highly abstract concept, and its ‘in principle’ effects are miniscule in real-life (because no object has infinite time or memory). Hence, it is not a profound property of reality. What counterargument David provides and what are its implications?
Indeed a virtual-reality generator that takes billions of years to compute is of little use. Usefulness of virtual reality and its real-life applications are crucial criterions for determining its profoundness.
Yet, rendering of certain properties was remarkably useful for evolution and science. It is because the rendered property doesn’t have to be ‘100% truthful or accurate’, it just has to be a better guess than the previous one. And this is another aspect of reality that allows renderings to be useful — we can successively improve our guesses (be it genes or theories). It also shows that one can improve based on the imperfect information, in fact, it will always be imperfect.
The previous successes of virtual rendering (in evolution and science) with its resource and information limitations imply the same for the universal virtual-reality generator — it is possible to build and use it with reasonable amount of resources.
On criticism:
to be at all useful or significant in the overall scheme of things, universality as I have defined it up to now is not sufficient. It merely means that the universal computer can eventually do what any other computer can. In other words, given enough time it is universal. But what if it is not given enough time? Imagine a universal computer that could execute only one computational step in the whole lifetime of the universe. Would its universality still be a profound property of reality? Presumably not. To put that more generally, one can criticize this narrow notion of universality because it classifies a task as being in a computer’s repertoire regardless of the physical resources that the computer would expend in performing the task. Thus, for instance, we have considered a virtual-reality user who is prepared to go into suspended animation for billions of years, while the computer calculates what to show next. In discussing the ultimate limits of virtual reality, that is the appropriate attitude for us to take. But when we are considering the usefulness of virtual reality - or what is even more important, the fundamental role that it plays in the fabric of reality - we must be more discriminating. — page 196
Counterargument and its implications:
Thus the fact that there are complex organisms, and that there has been a succession of gradually improving inventions and scientific theories (such as Galilean mechanics, Newtonian mechanics, Einsteinian mechanics, quantum mechanics, ... ) tells us something more about what sort of computational universality exists in reality. It tells us that the actual laws of physics are, thus far at least, capable of being successively approximated by theories that give ever better explanations and predictions, and that the task of discovering each theory, given the previous one, has been computationally tractable, given the previously known laws and the previously available technology. The fabric of reality must be, as it were, layered, for easy self-access. Likewise, if we think of evolution itself as a computation, it tells us that there have been sufficiently many viable organisms, coded for by DNA, to allow better-adapted ones to be computed (i.e. to evolve) using the resources provided by their worse-adapted predecessors. So we can infer that the laws of physics, in addition to mandating their own comprehensibility through the Turing principle, ensure that the corresponding evolutionary processes, such as life and thought, are neither too time-consuming nor require too many resources of any other kind to occur in reality.
So, the laws of physics not only permit (or, as I have argued, require) the existence of life and thought, they require them to be, in some appropriate sense, efficient. To express this crucial property of reality, modern analyses of universality usually postulate computers that are universal in an even stronger sense than the Turing principle would, on the face of it, require: not only are universal virtual-reality generators possible, it is possible to build them so that they do not require impracticably large resources to render simple aspects of reality. — page 196
9.3.0 What is the fundamental question of the computation complexity theory?
Just how efficiently can given aspects of reality be rendered? What computations, in other words, are practicable in a given time and under a given budget? This is the basic question of computational complexity theory which, as I have said, is the study of the resources that are required to perform given computational tasks. — page 197
9.3.1 How to distinguish between tractable and intractable computational tasks?
If the time it takes to execute a task grows exponentially (or sharply), then it is intractable.
What counts for ‘tractability’, according to the standard definitions, is not the actual time taken to multiply a particular pair of numbers, but the fact that the time does not increase too sharply when we apply the same method to ever larger numbers. … When we are multiplying the seven-digit numbers 4,220,851 and 2,594,209, each of the seven digits in 4,220,851 has to be multiplied by each of the seven digits in 2,594,209. So the total time required for the multiplication (if the operations are performed sequentially) will be seven times seven, or 49 microseconds. For inputs roughly ten times as large as these, which would have eight digits each, the time required to multiply them would be 64 microseconds, an increase of only 31 per cent. …
In the case we are considering, our computer would find the smaller of the two factors, 2,594,209, in just over a second. However, an input ten times as large would have a square root that was about three times as large, so factorizing it by this method would take up to three times as long. In other words, adding one digit to the input would now triple the running time. Adding another would triple it again, and so on. So the running time would increase in geometrical proportion, that is, exponentially, with the number of digits in the number we are factorizing. Factorizing a number with 25-digit factors by this method would occupy all the computers on Earth for centuries. — page 198, 199
Chaos Theory
9.4.0 What is the chaos theory? How it explains classical unpredictability?
Chaos theory states that almost all classical systems are extremely sensitive to initial conditions. Since in classical physics matter is continuous, one can never reach maximum preciseness, as there is no smallest unit of something (like a photon or quanta in quantum physics). Even with reasonable accuracy in initial measurements, differences between predicted and real outcomes tend to grow exponentially and irregularly, rendering predictions useless. Butterflies are mentioned so frequently not because they alone cause hurricanes, but because accurate prediction of weather require an impossibly high precision — to account for all negligible ‘butterfly’ details.
Chaos theory is about limitations on predictability in classical physics, stemming from the fact that almost all classical systems are inherently unstable. The ‘instability’ in question has nothing to do with any tendency to behave violently or disintegrate. It is about an extreme sensitivity to initial conditions. Suppose that we know the present state of some physical system, such as a set of billiard balls rolling on a table. If the system obeyed classical physics, as it does to a good approximation, we should then be able to determine its future behaviour - say, whether a particular ball will go into a pocket or not - from the relevant laws of motion, just as we can predict an eclipse or a planetary conjunction from the same laws. But in practice we are never able to measure the initial positions and velocities perfectly. So the question arises, if we know them to some reasonable degree of accuracy, can we also predict to a reasonable degree of accuracy how they will behave in the future? And the answer is, usually, that we cannot. The difference between the real trajectory and the predicted trajectory, calculated from slightly inaccurate data, tends to grow exponentially and irregularly (’chaotically’) with time, so that after a while the original, slightly imperfectly known state is no guide at all to what the system is doing. The implication for computer prediction is that planetary motions, the epitome of classical predictability, are untypical classical systems. In order to predict what a typical classical system will do after only a moderate period, one would have to determine its initial state to an impossibly high precision. Thus it is said that in principle, the flap of a butterfly’s wing in one hemisphere of the planet could cause a hurricane in the other hemisphere. The infeasibility of weather forecasting and the like is then attributed to the impossibility of accounting for every butterfly on the planet. — page 201
9.4.1 Is that so in reality?
Quantum theory describes reality to our best current knowledge. According to it, small differences in initial conditions cause only small differences in predicted outcomes.
However, real hurricanes and real butterflies obey quantum theory, not classical mechanics. The instability that would rapidly amplify slight mis-specifications of an initial classical state is simply not a feature of quantum-mechanical systems. In quantum mechanics, small deviations from a specified initial state tend to cause only small deviations from the predicted final state. — page 202
9.4.2 Why then can’t we make accurate predictions of the weather and systems alike?
It is because of the ‘spreading out’ effect in quantum physics. The perfect determinism of classical physics does not hold for any single universe.
The laws of quantum mechanics require an object that is initially at a given position (in all universes) to ‘spread out’ in the multiverse sense. — page 202
The butterfly flap would have no major impact on how the multiverse would play out. So if we take two groups of universes, one with wings up and the other with wings down, then the difference between the groups would be negligible. But within each group, every single universe would play out in widely different scenarios, for the reasons that have nothing to do with the butterfly! Due to the subjective perspective of the observers.
9.4.3 What are the differences between classical and quantum unpredictability?
In classical physics we can’t predict behavior of the system because we can’t measure it accurately enough, in fact, because it is continuous we would never be able to (number of zeros after decimal goes on forever).
Quantum physics is unpredictable because we don’t know in which universe we’ll be out of all possible ones.
For instance, a photon and its other-universe counterparts all start from the same point on a glowing filament, but then move in trillions of different directions. When we later make a measurement of what has happened, we too become differentiated as each copy of us sees what has happened in our particular universe. …
Classical systems are unpredictable (or would be, if they existed) because of their sensitivity to initial conditions. Quantum systems do not have that sensitivity, but are unpredictable because they behave differently in different universes, and so appear random in most universes. — page 202, 203
9.4.4 What is the differences between intractability and unpredictability?
Intractability is a problem that is always soluble in principle, as we just need more computational resources; unpredictability is insoluble even in principle.
Unpredictability has nothing to do with the available computational resources. … In neither case will any amount of computation lessen the unpredictability. Intractability, by contrast, is a computational-resource issue. It refers to a situation where we could readily make the prediction if only we could perform the required computation, but we cannot do so because the resources required are impractically large. — page 203
9.4.5 Is quantum system entirely unpredictable? Is it intractable?
Quantum system’s unpredictability can be misleading. Such experiments are unpredictable to us due to our subjective perspective, objectively, throughout the multiverse all possible outcomes of the experiment happen (we just get to see one out of possible scenarios).
In the double-slit experiment you don’t know where exactly the photon will appear this time, but you certainly can tell parts of the surfaces where it would never appear. Hence, when the photon is fired, in the multiverse it deterministically appears on every place of the surface where it could appear, yet, we perceive only one of those scenarios. We can’t predict which one we’ll observe of all the possible ones, but we can compute where it would never appear.
Photons can appear only in the green part. Every time we fire the photon in the multiverse it has been at every position in the green part, and never in the red. Yet, out of all those played out positions we perceive only one. We definitively know that is has been everywhere in the green part (we can predict it), but we can’t predict which one out of all we’ll perceive.
Calculating where is the green and red part gets intractable once we add more photons.
In the shadow experiments, a single photon passes through a barrier in which there are some small holes, and then falls on a screen. Suppose that there are a thousand holes in the barrier. There are places on the screen where the photon can fall (does fall, in some universes), and places where it cannot fall. To calculate whether a particular point on the screen can or cannot ever receive the photon, we must calculate the mutual interference effects of a thousand parallel-universe versions of the photon. Specifically, we have to calculate one thousand paths from the barrier to the given point on the screen, and then calculate the effects of those photons on each other so as to determine whether or not they are all prevented from reaching that point. Thus we must perform roughly a thousand times as much computation as we would if we were working out whether a classical particle would strike the specified point or not. — page 207
Mach-Zehnder Interferometer and Quantum Randomness
9.5.0 Are all quantum experiments random and make only probabilistic predictions?
No. Some of them predict a single, definite outcome.
9.5.1 Describe the Mach-Zehnder Interferometer experiment.
Mach-Zehnder interferometer is done with of two types of mirrors, the first one is normal, and the second one is half-silvered (those are used at police stations). Here is how it interacts with photons:
When a photon strikes such a mirror, it bounces off in half the universes, and passes straight through in the other half, as shown on next page:
The attributes of travelling in the X or Y directions behave analogously to the two voltages X and Y in our fictitious multiverse. So passing through the semi-silvered mirror is the analogue of the transformation above. And when the two instances of a single photon, travelling in directions X and Y, strike the second semi-silvered mirror at the same time, they undergo the transformation , which means that both instances emerge in the direction X: the two histories rejoin. To demonstrate this, one can use a set-up known as a ‘Mach-Zehnder interferometer’, which performs those two transformations (splitting and interference) in quick succession:
The two ordinary mirrors (the black sloping bars) are merely there to steer the photon from the first to the second semi-silvered mirror.
If a photon is introduced travelling rightwards (X) after the first mirror instead of before as shown, then it appears to emerge randomly, rightwards or downwards, from the last mirror (because then X⇒ X/Y, happens there). The same is true of a photon introduced travelling downwards (Y) after the first mirror. But a photon introduced as shown in the diagram invariably emerges rightwards, never downwards. By doing the experiment repeatedly with and without detectors on the paths, one can verify that only one photon is ever present per history, because only one of those detectors is ever observed to fire during such an experiment. Then, the fact that the intermediate histories X and Y both contribute to the deterministic final outcome X makes it inescapable that both are happening at the intermediate time. — The Beginning of Infinity, page 285
{ If you are struggling to understand, I highly recommend watching this video.}
9.6.0 How unpredictability and intractability can affect the universality of computation and simulation?
Unpredictability is of no problem — we can’t predict a fair roulette, but we sure can simulate it in virtual reality (i.e. compute). Yet intractable tasks are uncomputable, and hence are a barrier to our computation. On our classical computers we can’t compute or simulate accurately systems with quantum interference — they are intractable.
9.6.1 How has this given a rise to the field of quantum computation?
The intractability of quantum systems on classical computers might sound pessimistic at first, but it should not be so. For, if performing a quantum interference experiment is such a complex computation for the universe, we can do it and then record the results! And hence, harness huge amount of computation that universe does for us!
Instead of regarding the intractability of the task of rendering quantum phenomena as an obstacle, Feynman regarded it as an opportunity. If it requires so much computation to work out what will happen in an interference experiment, then the very act of setting up such an experiment and measuring its outcome is tantamount to performing a complex computation. Thus, Feynman reasoned, it might after all be possible to render quantum environments efficiently, provided the computer were allowed to perform experiments on a real quantum mechanical object. The computer would choose what measurements to make on an auxiliary piece of quantum hardware as it went along, and would incorporate the results of the measurements into its computations. — page 208
9.7.0 Reality is quantum: matter is discrete. Then, how can something that is only either 0 or 1 jump from one state to another?
First, we must challenge the premise, for as we’ve seen in chapter 2 (and chapter 11 in BoI) reality is inseparably a multiverse (one cannot separate it into independent single universes). So there is no ‘single-universe perspective’. What is happening is that within the multiverse, the object is transitioning from one state to another, going through a measure of 0% to 100%. So at one time it is in 25% of the multiverse transitioned to 1, then one instance later it is in the 50%, then 75% and so on (obviously we don’t yet have a good framework for thinking about time and quantum physics, as that would be the long-awaited quantum gravity theory).
Now let us look at the arrival of that single quantum of energy, to see how that discrete change can possibly happen without any discontinuity. Consider the simplest possible case: an atom absorbs a photon, including all its energy. This energy transfer does not take place instantaneously. (Forget anything that you may have read about ‘quantum jumps’: they are a myth.) There are many ways in which it can happen but the simplest is this. At the beginning of the process, the atom is in (say) its ‘ground state’, in which its electrons have the least possible energy allowed by quantum theory. That means that all its instances (within the relevant coarse-grained history) have that energy. Assume that they are also fungible. At the end of the process, all those instances are still fungible, but now they are in the ‘excited state’, which has one additional quantum of energy. What is the atom like halfway through the process? Its instances are still fungible, but now half of them are in the ground state and half in the excited state. It is as if a continuously variable amount of money changed ownership gradually from one discrete owner to another.
This mechanism is ubiquitous in quantum physics, and is the general means by which transitions between discrete states happen in a continuous way. In classical physics, a ‘tiny effect’ always means a tiny change in some measurable quantities. In quantum physics, physical variables are typically discrete and so cannot undergo tiny changes. Instead, a ‘tiny effect’ means a tiny change in the proportions that have the various discrete attributes. — The Beginning of Infinity, page 298
9.8.0 How does Shor’s algorithm work? What does it do?
This is an algorithm for factorizing a large number. All our current cryptography and cyber security is based on the simple fact that it is very easy to multiple two huge numbers, while extremely hard to factorize them back. This is an intractable calculation for our classical computers, but it isn’t for the quantum ones! All they have to do is to perform certain tasks in parallel and then share with each other the results through interference.
On number of universes cooperating:
When a quantum factorization engine is factorizing a 250-digit number, the number of interfering universes will be of the order of 10^500 - that is, ten to the power of 500. This staggeringly large number is the reason why Shor’s algorithm makes factorization tractable. I said that the algorithm requires only a few thousand arithmetic operations. I meant, of course, a few thousand operations in each universe that contributes to the answer. All those computations are performed in parallel, in different universes, and share their results through interference. — page 216
Simple example:
Imagine that for some computation we have to divide some big number by every number from 1 to a million. If we use classical computer we have to do it one at a time. If we use quantum computer we can split it into 10 universes (arbitrary choice, we could do 100, 1000 and so on) and perform the computation 10 times faster (or even faster depending on the number of chosen universes):
9.8.1 What are the implications of Shor’s algorithm on the interpretations of the quantum interference?
The only way to explain how Shor’s algorithm works is by appealing to the multiverse, otherwise there are simply not enough atoms in our universe:
To those who still cling to a single-universe world-view, I issue this challenge: explain how Shor’s algorithm works. I do not merely mean predict that it will work, which is merely a matter of solving a few uncontroversial equations. I mean provide an explanation. When Shor’s algorithm has factorized a number, using 10^500 or so times the computational resources that can be seen to be present, where was the number factorized? There are only about 10^80 atoms in the entire visible universe, an utterly minuscule number compared with 10^500. So if the visible universe were the extent of physical reality, physical reality would not even remotely contain the resources required to factorize such a large number. Who did factorize it, then? How, and where, was the computation performed? — page 217
😮 10 — The Nature of Mathematics
In this chapter we explore several questions:
Do abstract entities exist? Like the idea of a perfect circle.
How do we learn about abstract entities if no one has ever saw them?
What is Godel’s Incompleteness theorem?
What implications it has for mathematics?
Does Euclid’s axiom that triangle is 180° degrees hold in reality?
Summary
Abstract entities exist. They are abstract for they don’t have a physical representation yet. Like a perfect circle, or the next highest prime number that is currently not know to us, but we are actively searching for it. Something exist as long as it is a part of our best explanations of reality. Math, perfect circles, next highest unknown prime number, all exist.
Just as with any knowledge we learn about abstract entities through guesses and criticism of those guesses. In science we criticize experimentally, in mathematics proof plays that role. Laws of epistemology are universal, and they apply to our knowledge of math as well. If we have proven something, do we know it with 100% certainty? No!
Our brain is fallible, we use it to learn about mathematics, so even if we have proven something, we could always be mistaken. We could always have had misfirings of neurons which caused us to believe one over the other. Yes, it is very unlikely, but it doesn’t subtract from the fact that it is possible, so we can’t claim 100% certainty.
Mathematics had a crisis for they couldn’t agree what is the source of knowledge of mathematical entities. They struggled to understand how we learn about perfect circles without ever seeing one. They are of course making an empiricist mistake. We don’t need to observe anything, we always use our creativity to create knowledge be it about stars or circles.
Hilbert wanted to solve the ‘source problem’ by creating a number of fundamental mathematical inferences, so that every proof could be reduced to them. To everyone’s surprise Gödel proved its impossible! This is of course obvious when one thinks of mathematical knowledge the same way as of any other knowledge. Of course there is no rigid algorithm for creating knowledge, as it is always a creative process! One can’t just follow ‘a recipe’ — there isn’t one.
Mathematics is a study of the absolutely necessary truths (even independent from the laws of physics), but one never gets such certainty as a reward, for we always use our fallible brain.
You can practice chapter questions as flashcards here.
Abstract Entities
10.1.0 Do abstract entities, like numbers, exist? If so, in what way?
To answer this question in The Fabric of Reality David uses Dr. Johnson criterion:
Dr Johnson’s criterion (My formulation) If it can kick back, it exists. A more elaborate version is: If, according to the simplest explanation, an entity is complex and autonomous, then that entity is real. — page 96
However, his latest version for criterion of reality is: Something is real or exist in so far as it appears in our best explanations of reality. Is any explanation ruined by denying numbers existence? Mathematics appears in our best explanations of reality, and hence, it exists.
It seems intuitive that mathematical entities exist in a different way than physical ones, but explaining how exactly is something we are yet to form a good theory on.
10.1.1 How do we understand abstract entities?
Because they are intangible, we can’t conduct experiments as in regular science. In mathematics, proof plays the role of both experiment and explanation.
10.1.2 What is the difference between proof and experiment?
It is believed that once we prove something, we know with absolute certainty that it is true. Experiments can never imply this, its knowledge is always fallible.
We can perform a proof in the privacy of our own minds, or we can perform a proof trapped inside a virtual-reality generator rendering the wrong physics. Provided only that we follow the rules of mathematical inference, we should come up with the same answer as anyone else. And again, the prevailing view is that, apart from the possibility of making blunders, when we have proved something we know with absolute certainty that it is true. — page 224
10.1.3 Does proof imply that we know with absolute certainty that something is true?
The main thesis of the chapter is that it does not! Even mathematics is not safe from universality of laws of epistemology.
10.2.0 We never experience mathematical entities. No one ever saw a perfect circle, yet it is a clear concept in our mind. How do we obtain knowledge about it if no one ever experienced it?
Where does the certainty of a mathematical proof come from, if no one can perceive the abstract entities that the proof refers to? — page 227
Most mathematicians believe that scientific and mathematical knowledge comes from different sources. The source of the latter is mathematical intuition, it provides absolute certainty that scientists can never have, and allows us to argue about abstract entities that no one ever saw.
10.2.1 What is the problem with such source? Give example.
Mathematicians can’t agree on what it exactly means!
Obviously this is a recipe for infinite, unresolvable - controversy. — page 227
A prominent example are imaginary numbers. Some mathematicians used it to prove theorems about the distribution of prime numbers, others appealed to the invalidity of such tools. Reasoning of people that used imaginary numbers was as follows:
Why, they thought, should one not define new abstract entities to have any properties one likes? Surely the only legitimate grounds for forbidding this would be that the required properties were logically inconsistent. ... Admittedly, no one had proved that the system of imaginary numbers was self-consistent. But then, no one had proved that the ordinary arithmetic of the natural numbers was self-consistent either. — page 228
Similar debates have been about infinities.
10.2.2 Do we need to experience a perfect circle to understand it?
We don’t. Just as physicists understand distant stars they have never been to, so do mathematicians that have never been to perfect circles.
10.2.3 How our imperfect physical circles are related to the abstracted ones? How do we understand the latter ones?
We use our creativity and best explanations to understand abstract entities. This implies we could always be wrong, just as with studying anything physical.
The reliability of the knowledge of a perfect circle that one can gain from a diagram of a circle depends entirely on the accuracy of the hypothesis that the two resemble each other in the relevant ways. Such a hypothesis, referring to a physical object (the diagram), amounts to a physical theory and can never be known with certainty. But that does not, as Plato would have it, preclude the possibility of learning about perfect circles from experience; it just precludes the possibility of certainty. That should not worry anyone who is looking not for certainty but for explanations. …
[just as diagrams of perfect circle] The symbols too are physical objects - patterns of ink on paper, say - which denote abstract objects. And again, we are relying entirely upon the hypothesis that the physical behaviour of the symbols corresponds to the behaviour of the abstractions they denote. Therefore the reliability of what we learn by manipulating those symbols depends entirely on the accuracy of our theories of their physical behaviour, and of the behaviour of our hands, eyes, and so on with which we manipulate and observe the symbols. — page 241
Foundation of Mathematics (or its absence)
10.3.0 Disputes about imaginary numbers and infinities have put mathematics at crisis — there was no secure foundations of the subject. What Hilbert proposed to re-establish mathematical foundation?
Hilbert hoped to conclusively define a set of fundamental mathematical inferences, so that any proof could be checked against it and determined as valid or invalid. Set must fulfil two criterions. First, if the rules determine the proof as valid, they should never determine the proof with the opposite result as also valid. Second, the rules must prove themselves.
Hilbert’s plan was based on the idea of consistency. He hoped to lay down, once and for all, a complete set of modern rules of inference for mathematical proofs, with certain properties. They would be finite in number. They would be straightforwardly x applicable, so that determining whether any purported proof satisfied them or not would be an uncontroversial exercise. Preferably, the rules would be intuitively self-evident, but that was not an overriding consideration for the pragmatic Hilbert. He would be satisfied if the rules corresponded only moderately well to intuition, provided that he could be sure that they were self-consistent. That is, if the rules designated a given proof as valid, he wanted to be sure that they could never designate any proof with the opposite conclusion as valid. How could he be sure of such a thing? This time, consistency would have to be proved, using a method of proof which itself adhered to the same rules of inference. — page 233
10.3.1 What is Gödel’s Incompleteness theorem?
Hilbert was to be definitively disappointed. Thirty-one years later, Kurt Godel revolutionized proof theory with a root-and branch refutation from which the mathematical and philosophical worlds are still reeling: he proved that Hilbert’s tenth problem is insoluble. Godel proved first that any set of rules of inference that is capable of correctly validating even the proofs of ordinary arithmetic could never validate a proof of its own consistency. Therefore there is no hope of finding the provably consistent set of rules that Hilbert envisaged. Second, Godel proved that if a set of rules of inference in some (sufficiently rich) branch of mathematics is consistent (whether provably so or not), then within that branch of mathematics there must exist valid methods of proof that those rules fail to designate as valid. This is called Godel’s incompleteness theorem. To prove his theorems, Godel used a remarkable extension of the Cantor ‘diagonal argument’ that I mentioned in Chapter 6. He began by considering any consistent set of rules of inference. Then he showed how to construct a proposition which could neither be proved nor disproved under those rules. Then he proved that that proposition would be true. — page 234
10.3.2 What this discovery implies?
There will never be a fixed way of generating knowledge in mathematics, it will always rely on creativity of making new proofs! Just as experiments in science.
Thanks to Godel, we know that there will never be a fixed method of determining whether a mathematical proposition is true, any more than there is a fixed way of determining whether a scientific theory is true. Nor will there ever be a fixed way of generating new mathematical knowledge. Therefore progress in mathematics will always depend on the exercise of creativity. It will always be possible, and necessary, for mathematicians to invent new types of proof. They will validate them by new arguments and by new modes of explanation depending on their ever improving understanding of the abstract entities involved. Godel’s own theorems were a case in point: to prove them, he had to invent a new method of proof. I said the method was based on the ‘diagonal argument’, but Godel extended that argument in a new way. Nothing had ever been proved in this way before; no rules of inference laid down by someone who had never seen Godel’s method could possibly have been prescient enough to designate it as valid. — page 235
10.3.3 What distinction this implies in the knowledge creation about abstract and physical entities?
That there isn’t one! Laws of epistemology are universal and apply to both abstract and physical entities.
So explanation does, after all, play the same paramount role in pure mathematics as it does in science. Explaining and understanding the world - the physical world and the world of mathematical abstractions - is in both cases the object of the exercise. Proof and observation are merely means by which we check our explanations. — page 236
10.4.0 How proof is related to computation?
Proof that mathematicians use to get absolutely certain truth is just a computation that is performed on some physical object. Physical entities representing abstract ones (like symbols 1,+,68) are just our hypotheses. Scientific experiments can be seen as a computation of that kind. Our tools, such as senses and brain can always be fallible. Hence mathematicians don’t escape fallibility of knowledge any less than scientists!
Any physical experiment can be regarded as a computation, and any computation is a physical experiment. In both sorts of proof, physical entities (whether in virtual reality or not) are manipulated according to rules. In both cases the physical entities represent the abstract entities of interest. And in both cases the reliability of the proof depends on the truth of the theory that physical and abstract entities do indeed share the appropriate properties.
We can also see from the above discussion that proof is a physical process. In fact, a proof is a type of computation. ‘Proving’ a proposition means performing a computation which, if one has done it correctly, establishes that the proposition is true. — page 246
10.4.1 Should proof theory be a branch of mathematics?
It should not! It can only be a physical process, so it should be a part of science.
A very similar mis-classification has been caused by the fundamental mistake that mathematicians since antiquity have been making about the very nature of their subject, namely that mathematical knowledge is more certain than any other form of knowledge. Having made that mistake, one has no choice but to classify proof theory as part of mathematics, for a mathematical theorem could not be certain if the theory that justifies its method of proof were itself uncertain. But as we have just seen, proof theory is not a branch of mathematics - it is a science. Proofs are not abstract. There is no such thing as abstractly proving something, just as there is no such thing as abstractly calculating or computing something. — page 248
10.4.2 Proof can be regarded as an object and as a process. Which of the two is a more comprehensive representation?
Any proof is just a computation, it is referred to as an object when we can write the process of converting input into output on some physical matter, like a piece of paper. This criterion is always fulfilled in classical computation, yet it isn’t in quantum. If some computation can only be performed using interference and other universes, and there is no tractable way to verify the proof, then we can only rely on our process of setting up the computation. Hence, regarding proof as a process in a more comprehensive view.
consider some mathematical calculation that is intractable on all classical computers, but suppose that a quantum computer can easily perform it using interference between, say, 10^500 universes. To make the point more clearly, let the calculation be such that the answer (unlike the result of a factorization) cannot be tractably verified once we have it. The process of programming a quantum computer to perform such a computation, running the program and obtaining a result, constitutes a proof that the mathematical calculation has that particular result. But now there is no way of keeping a record of everything that happened during the proof process, because most of it happened in other universes, and measuring the computational state would alter the interference properties and so invalidate the proof. So creating an old-fashioned proof object would be infeasible; moreover, there is not remotely enough material in the universe as we know it to make such an object, since there would be vastly more steps in the proof than there are atoms in the known universe. This example shows that because of the possibility of quantum computation, the two notions of proof are not equivalent. The intuition of a proof as an object does not capture all the ways in which a mathematical statement may in reality be proved. — page 251
10.5.0 How Euclid’s axiom that triangle is 180° degrees have been refuted?
This is a staggering fact, but Einstein’s general theory of relativity showed that the sum of angles depends on the gravitational field within the triangle!
Einstein’s general theory of relativity included a new theory of geometry that contradicted Euclid’s and has been vindicated by experiment. The angles of a real triangle really do not necessarily add up to 180°: the true total depends on the gravitational field within the triangle. — page 247
10.5.1 What is the similar mistake that Turing has made? What did Feynman meant when he said: ‘He thought that he understood paper’?
we see the inadequacy of the traditional mathematical method of deriving certainty by trying to strip away every possible source of ambiguity or error from our intuitions until only self-evident truth remains. That is what Godel had done. That is what Church, Post and especially Turing had done when trying to intuit their universal models for computation. Turing hoped that his abstracted-paper-tape model was so simple, so transparent and well defined, that it would not depend on any assumptions about physics that could conceivably be falsified, and therefore that it could become the basis of an abstract theory of computation that was independent of the underlying physics. ‘He thought,’ as Feynman once put it, ‘that he understood paper.’ But he was mistaken. Real, quantum-mechanical paper is wildly different from the abstract stuff that the Turing machine uses. The Turing machine is entirely classical, and does not allow for the possibility that the paper might have different symbols written on it in different universes, and that those might interfere with one another. Of course, it is impractical to detect interference between different states of a paper tape. But the point is that Turing’s intuition, because it included false assumptions from classical physics, caused him to abstract away some of the computational properties of his hypothetical machine, the very properties he intended to keep. That is why the resulting model of computation was incomplete. — page 252
10.6.0 What is the main insight of the chapter?
Mathematics is the study of the absolutely necessary truths, yet our methods of understanding it are always fallible. Our physical reality just provides a narrow window from which we can observe the world of abstractions.
It follows that neither the theorems of mathematics, nor the process of mathematical proof, nor the experience of mathematical intuition, confers any certainty. Nothing does. Our mathematical knowledge may, just like our scientific knowledge, be deep and broad, it may be subtle and wonderfully explanatory, it may be uncontroversially accepted; but it cannot be certain. No one can guarantee that a proof that was previously thought to be valid will not one day turn out to contain a profound misconception, made to seem natural by a previously unquestioned ‘self-evident’ assumption either about the physical world, or about the abstract world, or about the way in which some physical and abstract entities are related. …
Unlike the relationships between physical entities, relationships between abstract entities are independent of any contingent facts and of any laws of physics. They are determined absolutely and objectively by the autonomous properties of the abstract entities themselves. Mathematics, the study of these relationships and properties, is therefore the study of absolutely necessary truths. In other words, the truths that mathematics studies are absolutely certain. But that does not mean that our knowledge of those necessary truths is itself certain, nor does it mean that the methods of mathematics confer necessary truth on their conclusions. After all, mathematics also studies falsehoods and paradoxes. And that does not mean that the conclusions of such a study are necessarily false or paradoxical.
Necessary truth is merely the subject-matter of mathematics, not the reward we get for doing mathematics. The objective of mathematics is not, and cannot be, mathematical certainty. It is not even mathematical truth, certain or otherwise. It is, and must be, mathematical explanation …
the fabric of physical reality provides us with a window on the world of abstractions. It is a very narrow window and gives us only a limited range of perspectives. — page 247, 252, 253, 255
🚧 11 — Time: The First Quantum Concept
🚧 12 — Time Travel
🏛️ 13 — The Four Strands
This chapter is a bit all over the place, but the main questions we tackle are:
What is Kuhn’s philosophy? What is its criticism?
What are the basics of rationality?
How quantum physics explains free will?
Summary
Kuhn explains science in paradigms — a set of beliefs and theories that generations of scientists hold. They are imprisoned in those theories and don’t change significantly ones opinions. Openness to criticism, non-authoritative values are all a myth. Once the evidence for the opposite theory accumulates, new generation of scientists begins to embrace it, mostly for selfish reasons as they would rise with new ideas succeeding. Past generation is no better, as they hold on to past theories for the same selfish reasons. Moreover, this theater of selfishness is for nothing, as no one paradigm is objectively better than the other, they are all relative, and all the fuss was for nothing — no real progress is ever made.
Obviously Kuhn is wrong, for claiming that science makes no objective progress is nonsense. General relativity not only makes objectively more accurate predictions, but also has objectively better explanations of reality. Kuhn’s entire philosophy is more likely to be associated with his own field of sociology, and his own frustration with it, not of all sciences.
Pragmatic instrumentalism is a variation of instrumentalism making the same mistake of disregarding the explanatory power of theories.
The essence of rationality is taking good explanations seriously and not discarding them light.
Individually, all four theories of this book have explanatory gaps, and are reductive. Yet, if one takes them mutually and seriously as explanations of the reality, a mesmerising, far more complete framework of the world is presented.
You can practice chapter questions as flashcards here.
13.1.0 Describe how science progresses according to Kuhn.
According to Kuhn, the scientific establishment is defined by its members’ belief in the set of prevailing theories, which together form a world-view, or paradigm. A paradigm is the psychological and theoretical apparatus through which its holders observe and explain everything in their experience. … Should any observation seem to violate the relevant paradigm, its holders are simply blind to the violation. When confronted with evidence of it, they are obliged to regard it as an ‘anomaly’, an experimental error, a fraud - anything at all that will allow them to hold the paradigm inviolate. Thus Kuhn believes that the scientific values of openness to criticism and tentativeness in accepting theories, and the scientific methods of experimental testing and the abandonment of prevailing theories when they are refuted, are largely myths that it would not be humanly possible to enact when dealing with any significant scientific issue.
…
he believes that science proceeds in alternating eras: there is ‘normal science’ and there is ‘revolutionary science’. During an era of normal science nearly all scientists believe in the prevailing fundamental theories, and try hard to fit all their observations and subsidiary theories into that paradigm. Their research consists of tying up loose ends, of improving the practical applications of theories, of classifying, reformulating and confirming. Where applicable, they may well use methods that are scientific in the Popperian sense, but they never discover anything fundamental because they never question anything fundamental. Then along come a few young troublemakers who deny some fundamental tenet of the existing paradigm. This is not really scientific criticism, for the troublemakers are not amenable to reason either. It is just that they view the world through a new and different paradigm. How did they come by this paradigm? The pressure of accumulated evidence, and the inelegance of explaining it away under the old paradigm, finally got through to them. …
an era of ‘revolutionary’ science begins. The majority, who are still trying to do ‘normal’ science in the old paradigm, fight back by fair means and foul - interfering with publication, excluding the heretics from academic posts, and so on. The heretics manage to find ways of publishing, they ridicule the old fogies and they try to infiltrate influential institutions. The explanatory power of the new paradigm, in its own terms (for in terms of the old paradigm its explanations seem extravagant and unconvincing) , attracts recruits from the ranks of uncommitted young scientists. There may also be defectors in both directions. Some of the old fogies die. Eventually one side or the other wins. If the heretics win, they become the new scientific establishment, and they defend their new paradigm just as blindly as the old establishment defended theirs; if they lose, they become a footnote in scientific history. In either case, ‘normal’ science then resumes. — page 322
13.1.1 What is the criticism of Kuhn’s philosophy?
First, taking one paradigm seriously doesn’t imply being imperceptible to other paradigms. Second, it disregards that switching of paradigms happens mainly due to their explanatory superiority. To counteract, Kuhn is forced to reject that there is any objective improvement in theories. This is clearly false. We can fly, our ancestors could only dream of it. Their paradigm is entirely different to ours, but to say they are incomparable is to deny the obvious.
But Kuhn is mistaken in thinking that holding a paradigm blinds one to the merits of another paradigm, or prevents one from switching paradigms, or indeed prevents one from comprehending two paradigms at the same time. …
as a description or analysis of the scientific process, Kuhn’s theory suffers from a fatal flaw. It explains the succession from one paradigm to another in sociological or psychological terms, rather than as having primarily to do with the objective merit of the rival explanations. Yet unless one understands science as a quest for explanations, the fact that it does find successive explanations, each objectively better than the last, is inexplicable.
Hence Kuhn is forced flatly to deny that there has been objective improvement in successive scientific explanations, or that such improvement is possible, even in principle:
there is [a step] which many philosophers of science wish to take and which I refuse. They wish, that is, to compare theories as representations of nature, as statements about ‘what is really out there’. Granted that neither theory of a historical pair is true, they nonetheless seek a sense in which the later is a better approximation to the truth. I believe that nothing of the son can be found. (in Lakatos and Musgrave (eds) , Criticism and the Growth of Knowledge, p. 265)
…
It is no good trying to pretend that successive explanations are better only in terms of their own paradigm. There are objective differences. We can fly, whereas for most of human history people could only dream of this. The ancients would not have been blind to the efficacy of our flying machines just because, within their paradigm, they could not conceive of how they work. The reason why we can fly is that we understand ‘what is really out there’ well enough to build flying machines. The reason why the ancients could not is that their understanding was objectively inferior to ours. — page 323, 324
13.1.2 Taking this criticism seriously, can one map Kuhn’s theory of science with the idea of objective progress?
David’s answer — no. It would still be inaccurate due to its romanticization of ‘geniuses’. Revolutionaries indeed create a lot of value, but the rest of the community significantly builds on their work, at times getting a better understanding than their originators.
If one does graft the reality of objective scientific progress onto Kuhn’s theory, it then implies that the entire burden of fundamental innovation is carried by a handful of iconoclastic geniuses. The rest of the scientific community have their uses, but in significant matters they only hinder the growth of knowledge. This romantic view (which is often advanced independently of Kuhnian ideas) does not correspond with reality either. — page 324
13.1.3 Describe Everett and Wheeler story that David uses to reject Kuhn’s philosophy.
Not only Wheeler helped Everett, but Everett’s innovation was not in rejecting the existing paradigm, but in taking it seriously.
On Wheeler:
Some twenty years later, Hugh Everett, then a Princeton graduate student working under the eminent physicist John Archibald Wheeler, first set out the many-universes implications of quantum theory. Wheeler did not accept them. He was (and still is) convinced that Bohr’s vision, though incomplete, was the basis of the correct explanation. But did he therefore behave as the Kuhnian stereotype would lead us to expect? Did he try to suppress his student’s heretical ideas? On the contrary, Wheeler was afraid that Everett’s ideas might not be sufficiently appreciated. So he himself wrote a short paper to accompany the one that Everett published, and they appeared on consecutive pages of the journal Reviews of Modern Physics. Wheeler’s paper explained and defended Everett’s so effectively that many readers assumed that they were jointly responsible for the content. Consequently the multiverse theory was mistakenly known as the ‘Everett-Wheeler theory’ for many years afterwards, much to Wheeler’s chagrin. — page 328
On taking quantum physics seriously:
the basis of Everett’s innovation was not a claim that the prevailing theory is false, but that it is true! The incumbents, far from being able to think only in terms of their own theory, were refusing to think in its terms, and were using it only instrumentally. Yet they had dropped the previous explanatory paradigm, classical physics, with scarcely a complaint as soon as a better theory was available. — page 330
13.2.0 What is pragmatic instrumentalism?
Using the theory without taking seriously its explanatory power.
If instrumentalism is the doctrine that explanations are pointless because a theory is only an ‘instrument’ for making predictions, pragmatic instrumentalism is the practice of using scientific theories without knowing or caring what they mean. — page 329
13.2.1 What made it a feasible philosophical movement in science?
Pragmatic instrumentalism has been feasible only because, in most branches of physics, quantum theory is not applied in its explanatory capacity. It is used only indirectly, in the testing of other theories, and only its predictions are needed. Thus generations of physicists have found it sufficient to regard interference processes, such as those that take place for a thousand-trillionth of a second when two elementary particles collide, as a ‘black box’: they prepare an input, and they observe an output. They use the equations of quantum theory to predict the one from the other, but they neither know nor care how the output comes about as a result of the input. — page 329
13.2.2 What are the two branches of physics that rely on the explanatory power of quantum physics and thus, can’t use it just instrumentally?
However, there are two branches of physics where this attitude is impossible because the internal workings of the quantum-mechanical object constitute the entire subject-matter of that branch. Those branches are the quantum theory of computation, and quantum cosmology (the quantum theory of physical reality as a whole). After all, it would be a poor ‘theory of computation’ that never addressed issues of how the output is obtained from the input! And as for quantum cosmology, we can neither prepare an input at the beginning of the multiverse nor measure an output at the end. Its internal workings are all there is. For this reason, quantum theory is used in its full, multiverse form by the overwhelming majority of researchers in these two fields. — page 330
13.3.0 What is the basic tenet of rationality according to David?
Good explanations should be taken seriously and not discarded lightly.
they violate a basic tenet of rationality - that good explanations are not to be discarded lightly. — page 331
13.4.0 How does quantum physics contribute to the notion of free will? How much free will depends on determinism and randomness of events?
Randomness is not desired as much as pure determinism isn’t. We want our actions to stem from who we are, our past thoughts and deeds, not some ‘coin-flips’. But not stem irreversibly so that we have no choice. There must be a golden middle.
Freedom has nothing to do with randomness. We value our free will as the ability to express, in our actions, who we as individuals are. Who would value being random? What we think of as our free actions are not those that are random or undetermined but those that are largely determined by who we are, and what we think, and what is at issue. (Although they are largely determined, they may be highly unpredictable in practice for reasons of complexity.) — page 338
Multiverse connects free will with physics by showing how it might be represented:
Consider this typical statement referring to free will: ‘After careful thought I chose to do X; I could have chosen otherwise; it was the right decision; I am good at making such decisions.’ In any classical world-picture this statement is pure gibberish. In the multiverse picture it has a straightforward physical representation, shown in Table 13.1. — page 339
13.5.0 What is the main thesis of the chapter? What is the explanation behind it?
The intellectual histories of the fundamental theories of the four strands contain remarkable parallels. All four have been simultaneously accepted (for use in practice) and ignored (as explanations of reality). One reason for this is that, taken individually, each of the four theories has explanatory gaps, and seems cold and pessimistic. [that is: Popperian epistemology, Everettian quantum physics, neo-Darwinian evolution and the theory of computation] To base a world-view on any of them individually is, in a generalized sense, reductionist. But when they are taken together as a unified explanation of the fabric of reality, this is no longer so. — page 343
🌌 14 — The Ends of the Universe
A big part of this chapter is centered around the omega-point idea. David in The Beginning of Infinity writes that such theories have been ruled out:
A small part of the revolution that is currently overtaking cosmology is that the omega-point models have been ruled out by observation. Evidence – including a remarkable series of studies of supernovae in distant galaxies – has forced cosmologists to the unexpected conclusion that the universe not only will expand for ever but has been expanding at an accelerating rate. Something has been counteracting its gravity. — The Beginning of Infinity, page 451
Nonetheless, it is still useful to analyze David’s hypothesizing. It is a great example of David taking an idea seriously, and letting its implications fully play out. If we want to understand the world we must have the courage to take our best scientific theories very seriously and we must have the boldness to uncover their implications. This is a perfect illustration of such intellectual bravery and boldness.
The essence of this chapter is whether laws of physics impose an upper bound on the computational steps in the universe, if not, knowledge creation could be an infinite process. Even though omega-point theory was ruled out, dark matter (whatever is counteracting gravity) could imply infinite computation in some other way — for now, we don’t know.
Summary
Knowledge indeed is growing both in depth and breadth, but depth is winning, so we’ll eventually converge to a single theory of everything (that would be the first theory of such kind). It wouldn’t be a unified theory of fundamental physics, as emergent phenomena would be left unexplained.
One should consider our best theories of reality both seriously and jointly, that is: quantum physics of the multiverse, Turing’s theory of universal computation, Neo-Darwinian evolution theory and Popperian epistemology.
It takes bravery and boldness to unravel what our best theories of the world imply, as you’ll have face the enemy of all progress — imprisoning, parochial social conventions.
You can practice chapter questions as flashcards here.
14.1.0 What are the two trends that David noticed while researching the book?
First, that human knowledge as a whole was continuing to take on the unified structure that it would have to have if it was comprehensible in the strong sense I hoped for. And second, that the unified structure itself was going to consist of an ever deepening and broadening theory of fundamental physics. — page 344
14.1.1 What is his opinion by the end of the book?
Knowledge indeed is growing both in depth and breadth, but depth is winning. Yet, it would not be a unified theory of fundamental physics, because an emergent phenomena would be left inexplicable.
The reader will know that I have changed my mind about the second point. The character of the fabric of reality that I am now proposing is not that of fundamental physics alone. For example, the quantum theory of computation has not been constructed by deriving principles of computation from quantum physics alone. It includes the Turing principle, which was already, under the name of the Church-Turing conjecture, the basis of the theory of computation. It had never been used in physics, but I have argued that it is only as a principle of physics that it can be properly understood. It is on a par with the principle of the conservation of energy and the other laws of thermodynamics: that is, it is a constraint that, to the best of our knowledge, all other theories conform to. But, unlike existing laws of physics, it has an emergent character, refer ring directly to the properties of complex machines and only consequentially to subatomic objects and processes. (Arguably, the second law of thermodynamics - the principle of increasing entropy - is also of that form.) Similarly, if we understand knowledge and adaptation as structure which extends across large numbers of universes, then we expect the principles of epistemology and evolution to be expressible directly as laws about the structure of the multiverse. That is, they are physical laws, but at an emergent level. Admittedly, quantum complexity theory has not yet reached the point where it can express, in physical terms, the proposition that knowledge can grow only in situations that conform to the Popperian pattern shown in Figure 3.3 But that is just the sort of proposition that I expect to appear in the nascent Theory of Everything, the unified explanatory and predictive theory of all four strands. — page 345
14.2.0 How should one consider the four theories when building ones world-view?
Creating a hierarchy of any kind between the theories leads only to a reductionist view with inexplicable gaps. Only when considered jointly, on equal terms, one can harness the fruits of a far more complete world-view.
Thus the problem with taking any of these fundamental theories individually as the basis of a world-view is that they are each, in an extended sense, reductionist. That is, they have a monolithic explanatory structure in which everything follows from a few extremely deep ideas. But that leaves aspects of the subject entirely unexplained. In contrast, the explanatory structure that they jointly provide for the fabric of reality is not hierarchical: each of the four strands contains principles which are ‘emergent’ from the perspective of the other three, but nevertheless help to explain them. — page 347
14.3.0 What is an Omegapoint theory?
It is a cosmological theory of the Big Crunch. It discovered that certain cosmological models with finite universe yield infinite space, time, memory capacity, number of possible computational steps and energy supply. David explains it from the Turing principle perspective.
The key discovery in the omega-point theory is that of a class of cosmological models in which, though the universe is finite in both space and time, the memory capacity, the number of possible computational steps and the effective energy supply are all unlimited. — page 348
14.3.1 How is this possible?
As we will approach singularity, fluctuations in changing the shape of the universe would increase without a limit, so that infinite number of variations would occur given finite time. Bending forces of the universe would provide unlimited energy. No matter will survive, but fundamental particles and gravity should. We can’t confirm or deny at the moment, but this might be enough to build the computer and provide infinite memory for it.
Both the amplitude and frequency of these oscillations [of the multiverse] would increase without limit as the final singularity was approached, so that a literally infinite number of oscillations would occur even though the end would come within a finite time. Matter as we know it would not survive: all matter, and even the atoms themselves, would be wrenched apart by the gravitational shearing forces generated by the deformed spacetime. However, these shearing forces would also provide an unlimited source of available energy, which could in principle be used to power a computer. How could a computer exist under such conditions ? The only ‘stuff ‘ left to build computers with would be elementary particles and gravity itself, presumably in some highly exotic quantum states whose existence we, still lacking an adequate theory of quantum gravity, are currently unable to confirm or deny. (Observing them experimentally is of course out of the question.) If suitable states of panicles and the gravitational field exist, then they would also provide an unlimited memory capacity, and the universe would be shrinking so fast that an infinite number of memory accesses would be feasible in a finite time before the end. The end-point of the gravitational collapse, the Big Crunch of this cosmology, is what Tipler calls the omega point. — page 349
14.3.2 What this implies if one applies Turing principle and unlimited computational steps?
Now, the Turing principle implies that there is no upper bound on the number of computational steps that are physically possible. So, given that an omega-point cosmology is (under plausible assumptions) the only type in which an infinite number of computational steps could occur, we can infer that our actual spacetime must have the omega-point form. Since all computation would cease as soon as there were no more variables capable of carrying information, we can infer that the necessary physical variables (perhaps quantum-gravitational ones) do exist right up to the omega point. — page 349
14.3.3 How does one infer the presence of an intelligent life at an Omega point?
Its fluctuations are violent and unpredictable (like classical chaos), to sustain the continuing computation (Turing principle) someone would have to steer the universe back on the ‘right track’. In principle, this steering is possible; it would require constant knowledge creation as the scope of the problem grows with time. Hence, to fulfil the Turing principle some intelligent beings must be present at an Omega point. This remarkable conclusion is just one of the example of inferences one can make when taking our best theories of reality seriously.
Since omega-point theory has been refuted, this entire inference is corrupted, but we could still draw insight from it:
You can’t judge ideas on the basis of ‘normalcy’ — this is a recipe for stagnation. They must be judged on the theories and explanations it stands upon.
Our best theories of reality must be taken seriously, only the brave ones can boldly embrace them averse parochial societal conventions and progress.
14.1 On geniuses, hypothesizing and bravery.7
14.4.0 Tipler infers that an intelligent life at the Omega point could ‘resurrect the dead’ by running the universe simulation from the Big Bang to the time that the person was born. He then concludes that this would be immoral for the ‘Omega point society’ not to resurrect all living beings from the past. What is the refutation of such reasoning?
Tipler is trying to predict the knowledge growth! But it is unpredictable — we don’t know what morality people have in the future.
it may seem natural to us that the omega-point intelligences, for reasons of historical or archaeological research, or com passion, or moral duty, or mere whimsy, will eventually create virtual-reality renderings of us, and that when their experiment is over they will grant us the piffling computational resources we would require to live forever in ‘heaven’. (I myself would prefer to be allowed gradually to join their culture.) But we cannot know what they will want. Indeed, no attempt to prophesy future large scale developments in human (or superhuman) affairs can produce reliable results. As Popper has pointed out, the future course of human affairs depends on the future growth of knowledge. And we cannot predict what specific knowledge will be created in the future - because if we could, we should by definition already possess that knowledge in the present. — page 359
14.2 Rebuttal.8
14.5.0 What is the reasoning difference between Tipler’s Omega point society and the existence of the Omega point?
The existence of an Omega point was a good theory because it confer well within our best explanations of reality. Inferring the existence of the Omega point theory was nothing more then taking our best theories and applying them universally. Tipler’s speculations of the moral landscape of Omega point society suffers from a fatal flaw — it tries to predict the growth of knowledge.
The whole story about what these far-future intelligences will or will not do is based on a string of assumptions. Even if we concede that these assumptions are individually plausible, the overall conclusions cannot really claim to be more than informed speculation. Such speculations are worth making, but it is important to distinguish them from the argument for the existence of the omega point itself, and from the theory of the omega point’s physical and epistemological properties. For those arguments assume no more than that the fabric of reality does indeed conform to our best theories, an assumption that can be independently justified. — page 358
14.6.0 What are the two closing thoughts of the book? What were the two theses that David wanted to defend and explain to the reader?
First, that the knowledge is growing both in depth and breadth, but first is winning, eventually converging to a unified theory of everything (which would have mistakes and be altered many times). Second, that our best scientific theories must be taken seriously and jointly to understand the world, that is: quantum physics of the multiverse, Turing’s theory of universal computation, Neo-Darwinian evolution theory and Popperian epistemology.
In view of all the unifying ideas that I have discussed, such as quantum computation, evolutionary epistemology, and the multiverse conceptions of knowledge, free will and time, it seems clear to me that the present trend in our overall understanding of reality is just as I, as a child, hoped it would be. Our knowledge is becoming both broader and deeper, and, as I put it in Chapter 1, depth is winning. But I have claimed more than that in this book. I have been advocating a particular unified world-view based on the four strands: the quantum physics of the multiverse, Popperian epistemology, the Darwin-Dawkins theory of evolution and a strengthened version of Turing’s theory of universal computation. It seems to me that at the current state of our scientific knowledge, this is the ‘natural’ view to hold. It is the conservative view, the one that does not propose any startling change in our best fundamental explanations. Therefore it ought to be the prevailing view, the one against which proposed innovations are judged. That is the role I am advocating for it. I am not hoping to create a new orthodoxy; far from it. As I have said, I think it is time to move on. But we can move to better theories only if we take our best existing theories seriously, as explanations of the world. — page 366
The end.
By Mark Kagach. Dedicated to my family and humanity: Where would I be without you?
we do not directly perceive the stars, spots on photographic plates, or any other external objects or events. We see things only when images of them appear on our retinas, and we do not perceive even those images until they have given rise to electrical impulses in our nerves, and those impulses have been received and interpreted by our brains. Thus the physical evidence that directly sways us, and causes us to adopt one theory or world-view rather than another, is less than millimetric: it is measured in thousandths of a millimetre (the separation of nerve fibres in the optic nerve), and in hundredths of a volt (the change in electric potential in our nerves that makes the difference between our perceiving one thing and perceiving another). — page 57
Thus solipsism, far from being a world-view stripped to its essentials, is actually just realism disguised and weighed down by additional unnecessary assumptions - worthless baggage, introduced only to be explained away. — page 83
Imagination is a straightforward form of virtual reality. What may not be so obvious is that our ‘direct’ experience of the world through our senses is virtual reality too. For our external experience is never direct; nor do we even experience the signals in our nerves directly - we would not know what to make of the streams of electrical crackles that they carry. What we experience directly is a virtual-reality rendering, conveniently generated for us by our unconscious minds from sensory data plus complex inborn and acquired theories (i.e. programs) about how to interpret them. — page 120
EX - INDUCTIVIST: But how could I have been so blind? To think that I once nominated Popper for the Derrida Prize for Ridiculous Pronouncements, while all the time he had solved the problem of induction! 0 mea culpa! God save us, for we have burned a saint! I feel so ashamed. I see no way out but to throw myself over this railing. — page 165
taken individually, each of the four theories has explanatory gaps, and seems cold and pessimistic. [that is: Popperian epistemology, Everettian quantum physics, neo-Darwinian evolution and the theory of computation] To base a world-view on any of them individually is, in a generalized sense, reductionist. But when they are taken together as a unified explanation of the fabric of reality, this is no longer so. — page 343
I was thinking about the question: How to build a better judgement? The reasoning above provided an interesting definition:
judgement — the accuracy of ones virtual rendering of the external world
It is not reductive, the accuracy encompasses everything from experiments of fundamental physics to understanding emotions of other people. But this picture is not complete. Judgement is also about ones actions:
judgement — the accuracy of ones virtual rendering of the external world and how ones actions will influence it (both in the long and short run)
Willpower, in that case, is about actually doing the right thing.
discovering the physics of an environment depends on creating a virtual-reality rendering of it. Normally one would say that scientific theories only describe and explain physical objects and processes, but do not render them. For example, an explanation of eclipses of the Sun can be printed in a book. A computer can be programmed with astronomical data and physical laws to predict an eclipse, and to print out a description of it. But rendering the eclipse in virtual reality would require both further programming and further hardware. However, those are already present in our brains! The words and numbers printed by the computer amount to ‘descriptions’ of an eclipse only because someone knows the meanings of those symbols. That is, the symbols evoke in the reader’s mind some sort of likeness of some predicted effect of the eclipse, against which the real appearance of that effect will be tested. Moreover, the ‘likeness’ that is evoked is interactive. One can observe an eclipse in many ways: with the naked eye, or by photography, or using various scientific instruments; from some positions on Earth one will see a total eclipse of the Sun, from other positions a partial eclipse, and from any where else no eclipse at all. In each case an observer will experience different images, any of which can be predicted by the theory. What the computer’s description evokes in a reader’s mind is not just a single image or sequence of images, but a general method of creating many different images, corresponding to the many ways in which the reader may contemplate making observations. In other words, it is a virtual-reality rendering. Thus, in a broad enough sense, taking into account the processes that must take place inside the scientist’s mind, science and the virtual-reality rendering of physically possible environments are two terms denoting the same activity. — page 118
I understand David’s definition, but I would like to have a way to quantify the virality factor of a replicator. Clearly some songs are more viral than others — they cause themselves to be replicated more than their rivals, yet David doesn’t mention a measure for that.
I understand David’s point on copying genes instead of organisms, therefore organism is an environment, not a replicator. I believe that sometimes seeing an organisms as a replicator is useful, it is just a higher scale.
Yes, the exact organism would not be copied, but neither are genes — they are made of out of atoms and those get copied. Genes are just environments for true replicators — atoms (we can then consider protons, neutrons and so on)! I am not sure in the validity of this reasoning, but I want to point it out.
Organisms, just as genes, can’t replicate without an environment: a bear needs a partner-bear to reproduce. I believe we can take even higher scale: a habitat consists of organisms, if they are genes, then habitat is an environment. A habitat can die out (collapse) if it doesn’t have the right balance of organisms (genes), for every species performs some function. Just as without a crucial gene an organism dies, a habitat collapses without certain organisms. Around 20-30 million people have died during the Four Pests campaign. I can also argue that Rapa Nui ‘habitat’ (that David mentions in chapter 17 of The Beginning of Infinity) has collapsed because of absence of necessary organisms (or genes).
I think that moving along the stack of sizes, be it genes or habitats, provides useful insights. I am not sure how accurately they resemble the replicator idea, but they shed a new perspective. Just as virtual reality and evolution analogy that David makes in 8.7.0 card.
{8.4 Turing principle: It is possible to build a virtual-reality generator whose repertoire includes every physically possible environment. This implies that there could be a knower who understood reality sufficiently well. Revisit card 6.4.0 for details.}
In chapter 8 David explains how knowledge bearing genes are more spread across the universe and form some structure compared to non-knowledge bearing ones. Why can’t we apply the same idea to moral and aesthetic values? Some, are more knowledgeable (or knowledge-bearing) than others, they tend to survive (withstand), across space, time and universes.
Hence, some moral and aesthetic claims are objectively better than others — they are more represented across the multiverse.
Thus, if one wants to find out which moral and aesthetic values are more knowledgeable (closer to truth), one just needs to get a god-eye-view of the multiverse; the bigger the structure, the closer to truth it is.
One counterargument to that reasoning can be that multiverse is infinite, and thus this is a meaningless comparison, any part of it is just as big as any other. Hence, every moral claim is represented with equal measure across it, in fact, every possible moral or aesthetical claim is just as well represented as any other. Probabilities just don’t work with infinities.
However, we can describe probabilities in infinities through measures. Thus, argument stands.
This is one of the best illustrations of David’s reasoning capabilities. It is not that David had some genius-type insight, he just took our best theories of the world very seriously, and then he had the boldness and bravery to unravel what they actually imply, all while staring directly in the face of parochial social conventions. Not only he had the courage to let the ideas play out, but he had the courage to share them. Sometimes ‘geniusness’ is about just letting the ideas guide the path for you.
Let’s assume that omega point theory is true, and there will be society living during its collapse. A rebuttal to the David’s response would be that if multiverse is infinite, then there clearly are universes where all dead are resurrected because it is physically possible. But once again, the validity of this argumentation relies on whether multiverse consists of infinite universes, or just many many many universes. Inspired by: Disagreements with Deutsch: The Afterlife}